线性代数基础
第一章 行列式
1.1 二阶行列式定义
定义1 记号 $\begin{vmatrix}a_{11} & a_{12} \\a_{21} & a_{22}\end{vmatrix}$ 表示代数和 $a_{11}a_{22} - a_{12}a_{21}$,称为 二阶行列式 即:
$$ \begin{align*} \begin{vmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{vmatrix} &= a_{11}a_{22} - a_{12}a_{21} \end{align*} $$ $a_{ij}$:称为 $(i, j)$ 元素;$i$: 行标;$j:$列标。比如上方的 $a_{12}$ 里面的$1$是行标,$2$是列标。那么 $a_{12}$ 称为$(1, 2)$元素。
行:r(row)
列:c(colum)
1.1 对角线法则
从左上角到右下角的连线,叫主对角线。即$a_{11}$和$a_{22}$。
从右上角到左下角的连线,叫副对角线。即$a_{12}$和$a_{21}$。
那么这个二阶行列式,就等于主对角线元素的乘积减去副对角线的乘积。
1.2 二元线性方程组
给定二元线性方程组:$\begin{cases}a_{11}x_1 + a_{12}x_2 = b_1, \quad \text{(1)} \\a_{21}x_1 + a_{22}x_2 = b_2, \quad \text{(2)}\end{cases}$
使用消元法,我们可以通过以下步骤求解:
- 从方程 (1) 乘以 $a_{22}$ 并从方程 (2) 乘以 $a_{12}$,然后相减,消去 $x_2$:
同样,从方程 (2) 乘以 $a_{11}$ 并从方程 (1) 乘以 $a_{21}$,然后相减,消去 $x_1$:
$$ (a_{11}a_{22} - a_{12}a_{21})x_2 = a_{11}b_2 - b_1a_{21} $$如果 $a_{11}a_{22} - a_{12}a_{21} \neq 0$,则方程组有唯一解:
$$ x_1 = \frac{b_1a_{22} - a_{12}b_2}{a_{11}a_{22} - a_{12}a_{21}}, \quad x_2 = \frac{a_{11}b_2 - b_1a_{21}}{a_{11}a_{22} - a_{12}a_{21}} $$这样,我们就得到了二元线性方程组的唯一解。如果$a_{11}a_{22} - a_{12}a_{21} = 0$,则方程组可能没有解或者有无限多解,这取决于其他系数的值。
如果这个分式可以用二元线性方程组来进行表达的话,是否会在计算上变得特别方便呢?
1.3 系数行列式
对照上方的二元线性方程组的解$x_1$、$x_2$。
观察分母要写成二元线性方程组的形式,恰好是这个二元线性方程组的系数构成的一个二阶行列式。所以,我们说把系数提出来所组成的行列式,称为系数行列式。
记作:
$$ D=\begin{align*}\begin{vmatrix}a_{11} & a_{12} \\a_{21} & a_{22}\end{vmatrix}&= a_{11}a_{22} - a_{12}a_{21}\end{align*} $$再观察$x_1$、$x_2$的分子
先来看$x_1$的分子,分子与分母进行比较就会发现,系数行列式$D_1$的第一列恰好换成了,二元线性方程组的右边的常数项$b_1$、$b_2$。也就是
$$ \begin{cases}b_{1}x_1 + a_{12}x_2 = b_1, \quad \text{(1)} \\b_{2}x_1 + a_{22}x_2 = b_2, \quad \text{(2)}\end{cases} $$则有:
$$ D_1=\begin{align*}\begin{vmatrix}b_{1} & a_{12} \\b_{2} & a_{22}\end{vmatrix}&= b_{1}a_{22} - a_{12}b_{2}\end{align*} $$同样的再来看$x_2$的分子,系数行列式$D_2$的第二列恰好换成了,二元线性方程组的右边的常数项$b_1$、$b_2$。也就是
$$ \begin{cases}b_{1}x_1 + b_{1}x_2 = b_1, \quad \text{(1)} \\b_{2}x_1 + b_{2}x_2 = b_2, \quad \text{(2)}\end{cases} $$ $$ D_2=\begin{align*}\begin{vmatrix}a_{11} & b_{1} \\a_{21} & b_{2}\end{vmatrix}&= a_{11}b_{2} - b_{1}a_{21}\end{align*} $$于是,在$D\neq0$时,有
$$ x_{1}=\frac{D_1}{D},x_{2}=\frac{D_2}{D} $$这样,有了二阶行列式,在计算二元线性方程组的时候。就会非常方便。
例:解方程组
$$ \begin{cases}2x_1 + 4x_2 = 1, \quad \text{(1)} \\x_1 + 3x_{2} = 2, \quad \text{(2)}\end{cases} $$首先,我们把二元线性方程组的系数的位置提出来,并且不改变它们的位置,得到
$$ \because D=\begin{align*}\begin{vmatrix}2 & 4 \\1 & 3\end{vmatrix}\end{align*}=2\times3-4\times1=2\neq 0 $$在系数行列式为零的时候,方程组有唯一的解。
$$ \therefore x_{1}=\frac{D_1}{D},x_{2}=\frac{D_2}{D} $$那么我们来计算
$$ D_1=\begin{align*}\begin{vmatrix}1 & 4 \\2 & 3\end{vmatrix}\end{align*}=1\times 3-4\times 2 = -5 $$类似的
$$ D_2=\begin{align*}\begin{vmatrix}2 & 1 \\1 & 2\end{vmatrix}\end{align*}=2\times 2-1\times 1 = 3 $$代入$x_1$、$x_2$ 中
$$ x_{1}=\frac{D_1}{D}=-\frac{5}{2},x_{2}=\frac{D_2}{D}=\frac{3}{2} $$1.4 三阶行列式定义
定义2 记号$
\begin{align*}
\begin{vmatrix}
a_{11} & a_{12} & a_{13} \
a_{21} & a_{22} & a_{23} \
a_{31} & a_{32} & a_{33} \
\end{vmatrix}
\end{align*}
$代表代数和
这个代数和是六项,三个加法,三个减法。这个记号,我们叫称为:三阶行列式。
即:
$$ \begin{align*} \begin{vmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \\ \end{vmatrix} \end{align*}=\\a_{11}a_{22}a_{33}+a_{12}a_{23}a_{31}+a_{13}a_{21}a_{32}\\-a_{13}a_{22}a_{31}-a_{11}a_{23}a_{32}-a_{12}a_{21}a_{33} $$1.5 三阶行列式的计算方法:
1.5.1 对角线法则
三阶行列式也有对角线法则:从左上角到右下角的连线,我们称为主对角线,凡是与对角线平行的,我们都取正号。平行指的是,我们在取每一项的时候要取自不同行,不同列的三个元素的乘积。我们取的时候,尽量从小到大的取,这样比较有规律,不容易拉下。也就是说,先取第一行,再取第二行,再取第三行。此时列也是取不同的列。
从右上角到左下角的连线,我们称为副对角线。凡是与副对角线平行的,我们都取负号。
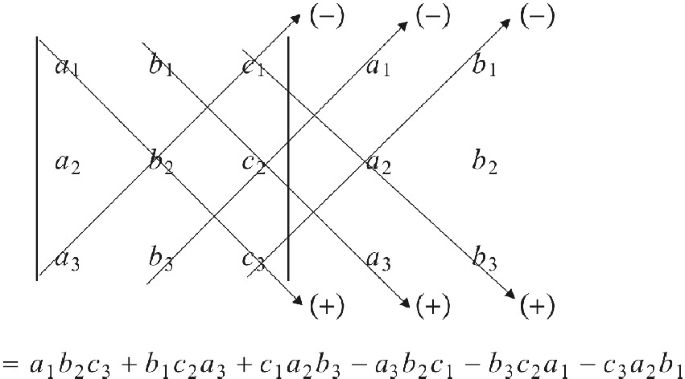
1.5.2 沙路法则
沙路法则就是把三阶行列式的前两列,写到三阶行列式的右侧:
$$ \begin{align*} \begin{vmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \\ \end{vmatrix} \begin{matrix} a_{11} & a_{12} \\ a_{21} & a_{22} \\ a_{31} & a_{32} \\ \end{matrix} \end{align*}=\\a_{11}a_{22}a_{33}+a_{12}a_{23}a_{31}+a_{13}a_{21}a_{32}\\-a_{13}a_{22}a_{31}-a_{11}a_{23}a_{32}-a_{12}a_{21}a_{33} $$凡是和主对角线平行的,我们都去正。
例 求$\begin{vmatrix}2 & 1 & 2 \\-4 & 3 & 1 \\2 & 3 & 5\end{vmatrix}$的值。
解:$\begin{align}&\begin{vmatrix}2 & 1 & 2 \\-4 & 3 & 1 \\2 & 3 & 5\end{vmatrix}\\&=2\times3\times5+1\times1\times2+2\times(-4)\times3-2\times3\times2-1\times(-4)\times5-2\times1\times3\\&=30+2-24-12+20-6\\&=10\end{align}$
有了三阶行列式,在计算三元线性方程组的时候,就会非常方便。
例子:讨论三元线性方程组
$$ \begin{cases} a_{11}x_{1}+a_{12}x_{2}+a_{13}x_{3}=b_1\\ a_{21}x_1+a_{22}x_2+a_{23}x_{3}=b_{2}\\ a_{31}x_{1}+a_{32}x_2+a_{33}x_{3}=b_3 \end{cases} $$记
$$ D=\begin{vmatrix} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{33}\\ a_{31} & a_{32} & a_{33} \end{vmatrix} $$解:当系数行列式$D$不为零的时候,有唯一的解。$x_i=\frac{D_i}{D}$
$$ D_1=\begin{vmatrix} b_{1} & a_{12} & a_{13}\\ b_{2} & a_{22} & a_{33}\\ b_{3} & a_{32} & a_{33} \end{vmatrix} , D_2=\begin{vmatrix} a_{11} & b_{1} & a_{13}\\ a_{21} & b_{2} & a_{33}\\ a_{31} & b_{3} & a_{33} \end{vmatrix} , D_3=\begin{vmatrix} a_{11} & a_{12} & b_{1}\\ a_{21} & a_{22} & b_{2}\\ a_{31} & a_{32} & b_{3} \end{vmatrix} $$ $D_1$相当于系数行列式$D$的第一列换成方程组的最右边的常数项,$D_2$、$D_3$类似。于是,当$D\neq0$的时,有$x_1=\frac{D_1}{D}$,$x_2=\frac{D_2}{D}$,$x_3=\frac{D_3}{D}$
例:解线性方程组$$ \begin{cases} 2x_1-x_2+x_3=0\\ 3x_1+2x_2-5x_3=1\\ x_1+3x_2-2x_3=4 \end{cases} $$。
解:$\because D=\begin{vmatrix}2&-1&1\\3&2&-5\\1&3&-2\end{vmatrix}=28\neq0$
$$ \because D_1=\begin{vmatrix} 0 & -1 & 1\\ 1 & 2 & -5\\ 4 & 3 & -2 \end{vmatrix}=13 , D_2=\begin{vmatrix} 2 & 0 & 1\\ 3 & 1 & -5\\ 1 & 4 & -2 \end{vmatrix}=47 , D_3=\begin{vmatrix} 2 & -1 & 0\\ 3 & 2 & 1\\ 1 & 3 & 4 \end{vmatrix}=21 $$ $$ \therefore x_1=\frac{D_1}{D}=\frac{13}{28},x_2=\frac{D_2}{D}=\frac{47}{28},x_3=\frac{D_3}{D}=\frac{21}{28}=\frac{3}{4} $$二阶行列式可以解出二元线性方程组,三阶行列式可以解出三元线性方程组。那么有一个$N$元线性方程组,我们想解出它的话,我们是不是应该给出$N$阶行列式?那么我们要给出$N$阶行列式的话,我们首先需要介绍,什么是全排列,什么是逆序数。
课堂练习
【当选题】计算三阶行列式$\begin{vmatrix}1&1&0\\1&2&0\\0&0&3\end{vmatrix}$的值为()
A. 3
B. -3
C. 0
D. 1
正确答案:A
1.6 小结
本章我们介绍行列式怎么计算,给出了对角线法则,介绍了三阶行列式怎么计算。每项式取行列式的不同行不同列的乘积。有正有负。
练习1
计算行列式 $D=\begin{vmatrix}1&2&3\\4&0&5\\-1&0&6\end{vmatrix}$
解方程 $D=\begin{vmatrix}1&1&1\\2&3&x\\4&9&x^2\end{vmatrix}=0$
思考对角线法则、沙路法则三阶以上可用吗?
第二章、全排列及其逆序数
2.1 全排列定义
把 $n$ 个不同的元素排成的一列,称为这 $n$ 个元素的一个全排列,简称排列。
把 $n$ 个不同的元素排成一列,共有$P_n$种排法。
例如:$P_3=3!=3\times2\times1=6$,也就是三个数进行全排列,则它有6种排法。
例如:1、2、3的全排列。排法有:
123、132
213、231
312、321
共有$3\times2\times1=6$种,即$P_3=3\times2\times1=6$
类似的,$n$个数进行全排列的话。$P_n$就应该有多少种排法?
$$ P_n=n\times(n-1)\cdots\times3\times2\times1=n! $$应该是$n$的阶乘种排法。
2.2 逆序数定义
规定 标准次序:标由小到大的排列。
定义:在 $n$ 个元素的一个排列中,若 某两个元素排列的次序与标准次序不同,就称这两个数构成一个逆序。一个排列中所有逆序的总和称为这个排列的逆序数,记
$$ N(p_1p_2 \cdots p_n)或t(p_1p_2 \cdots p_n) $$例:$N(1234)=0$
相当于 $1234$ 这个排列的逆序数,是0。为什么?
因为$1234$是标准次数,它没有逆序数,所以逆序数是0。
例:$N(1243)=1$
$1243$和标准次序$1234$对比,$43$颠倒了。所以它的逆序数是1。一个排列的逆序数的计算方法:
设$p_1,p_2,\cdots,p_n$是$1,2,\cdots,n$的一个排列,用 $t_i$ 表示元素,$p_i$的逆序数。即排在$p_i$前面并比$p_i$大的元素有$t_i$个。
比如$p_1$的逆序数就记成$t_1$,$p_2$前面并比$p_2$大的元素有$t_2$个,以此类推。$p_n$的逆序数,就记成$t_n$。
$t_n$最大取多少?它是不是表示$p_n$前面比$p_n$大的元素,那么$p_n$ 前面,有多少个?$n-1$个。所以$t_n$最大就是$n-1$。那么所有的这些$t_1$、$t_2$加在一起,则 排列的逆序数为:
$$ t=t_1+t_2+\cdots+t_n $$例:求排列$32514$的逆序数。
解:
先算出第一个3,3前面比3大的有0个。所以
$t_1=0$再看看2,2前面比2大的元素有1个,所以
$t_2=1$再看看5,5前面比5大的元素有0个,所以
$t_3=0$再看看1,1前面比1大的元素有3个,所以
$t_4=3$再看看4,4前面比4大的元素有1个,所以
$t_5=1$因此排列$32514$的逆序数为
$$ \begin{align} t&=t_1+t_2+t_3+t_4+t_5\\&=0+1+0+3+1\\&=5 \end{align} $$2.3 排列的奇偶性
逆序数为奇数的排列称为奇排列,逆序数为偶数的排列称为偶排列
例:
$123$ 逆序数 $t=0$ 为偶排列 $321$ 逆序数 $t=3$ 为奇排列 $312$ 逆序数 $t = 2$ 为偶排列例:求排列 $n(n-1)\cdots 321$ 的逆序数,并讨论其奇偶性。
解:
$n$ 前面比它大的数有几个?0 $n-1$前面比它大的数有几个?1个 $n-2$前面比它大的数有几个?2个以此类推
$1$ 前面比它大的数有几个?(n-1)个我们可以利用等差数列求和$S_n=\frac{n}{2}(a_1+a_n)$。得到和是$\frac{n(n-1)}{2}$
$$ \begin{align}N(n(n-1)\cdots321)&=0+1+2+\cdots+(n-1)\\&=\frac{n(n-1)}{2}\end{align} $$我们尝试试几个数
$n=0$,逆序数$N=0$ $n=1$,逆序数$N=0$ $n=2$,逆序数$N=1$ $n=3$,逆序数$N=3$ $n=4$,逆序数$N=6$ $n=5$,逆序数$N=10$可以发现规律,这个逆序数是两奇、两偶的,四个一循环。所以它的逆序数与周期有关。
当$n=4k$,或$4k+1$的时候,$N_1=2k(4k-1)$为偶数,$N2=2k(4k+1)$为偶数。
当$n=4k+2$,或$4k+3$的时候,$N_3=(2k+1)(4k+1)$为奇数,$N_4=(2k+1)\frac{4k+3}{2}$为奇数。
记住该结论,该结论在后面还会用到。
课堂练习:
【判断题】排列$n(n-1)(n-2)\cdots3\cdot2\cdot1$的逆序数是$\frac{n(n-1)}{2}$。
A. 对
B. 错
正确答案:A
2.4 小结
本章我们学习了三个内容:
1、什么是全排列
2、什么是逆序数
怎么算一个排列的逆序数。这是我们这部分学习的重点。
3、排列的奇偶性
逆序数是奇数就是奇排列,逆序数是偶数就是偶排列。
练习:
求下面排列的逆序数:
(1)2 3 4 5 1 6
(2)3 4 1 5 6 2
(3)6 5 4 3 2 1
第三章 n阶行列式
回顾
$$ \begin{vmatrix}a_{11}&a_{12}\\a_{12}&a_{21}\end{vmatrix}=a_{11}a_{22}-a_{12}a_{21},\begin{align}N(12)=0,偶排列(取正号)\\N(21)=1,奇排列(取负号)\end{align} $$ $$ \begin{vmatrix}a_{11}&a_{12}& a_{13}\\a_{21}&a_{22}& a_{23}\\a_{31}&a_{32}&a_{33}\end{vmatrix}=\begin{align}a_{11}a_{22}a_{33}+a_{12}a_{23}a_{31}+a_{13}a_{21}a_{32}\\-a_{13}a_{22}a_{31}-a_{11}a_{23}a_{32}-a_{12}a_{21}a_{33}\end{align},\begin{cases}偶排列(取正号)\begin{cases}N(123)=0\\N(231)=2\\N(312)=2\end{cases}\\奇排列(取负号)\begin{cases}N(132)=1\\N(213)=1\\N(321)=3\end{cases}\end{cases} $$所以,我们就有一个统一的规律。行标写成标准次序的时候由列标的逆序数来定它前面的符号。列标的排列如果是奇排列的话符号取负号,列标的排列如果是偶排列的话符号取正号。
二阶行列式计算出来的是两项,两项相当于是2的阶乘项目,即共$2!$项。
二阶行列式计算出来的是六项,六项相当于是3的阶乘项目,即共$3!$项。
为什么是这个阶乘项呢?
因为三阶行列式算的时候,那个列标相当于123的某个排列,一共是$3!$种排列。
那么$n$阶行列式,应该有多少项?应该是$n!$项。
观察二、三阶行列式,得出下面结论:
每项都是不同行不同列的$n$个元素的乘积。
$n$阶行列式是$n!$项的代数和。每项符号:当行标按自然顺序排列后,由列标排列的奇偶性确定:奇排列取负号、偶排列取正号。
故:
$$ \begin{align} D_3&=\begin{vmatrix}a_{11} & a_{12} & a_{13}\\a_{21} & a_{22} & a_{23}\\a_{31}&a_{32}&a_{33}\end{vmatrix}\\&=\sum_{j_1j_2j_3}(-1)^ta_{1j_1}a_{2j_2}a_{3j_3},t=N(j_1j_2j_3) \end{align} $$一个三阶行列式,可以写成一个sigma和,这个和一共多少项呢? 是$3!$项。每一项是什么呢?是$-1$的$t$次方,$a_{1j_1}$、$a_{2j_2}$、$a_{3j_3}$,相当于行标$123$写成标准次序,列标$j_1j_2j_3$就是$123$的某个排列。前面的符号$-1$的$t$次方由谁来定?由列标$j_1j_2j_3$的逆序数来定,它要是奇数前面取负号,它要是偶数前面取正号。那么这个行列式就可以写成三个阶乘项的和。
那么类推n阶行列式是否可以类似的给出定义呢?
3.1 n阶行列式定义
定义:$n!$ 项 $(-1)^t a_{1p_1} a_{2p_2}\cdots a_{np_n}$的和,其中$t=N(p_1p_2 \cdots p_n)$,若逆序数$t$是奇数前面取负号,若逆序数$t$是偶数前面取正号。记作:
$$ \sum(-1)^ta_{1p_1}a_{2p_2} \cdots a_{np_n},t=N(p_1p_2 \cdots p_n) $$称为$n$阶行列式。
$D_n$ 相当于 $n$ 方个元素,不改变位置两边画上竖线。记作: $$ \begin{align} D_n&=\begin{vmatrix}a_{11} & a_{12} & \cdots & a_{1n}\\a_{21} & a_{22} & \cdots & a_{2n}\\ \vdots & \vdots & \vdots & \vdots \\a_{n1} & a_{n2} & \cdots & a_{nn}\end{vmatrix}\\&=\sum(-1)^t a_{1p_1} a_{2p_2} \cdots a_{np_n} \end{align} $$n阶行列式的另一种记法,因为n阶行列式的英文叫:Determinant。
前三个字母 $Det(a_{ij})$ 或者 $|a_{ij}|$ 。但是由这两个符号来表示,是看不出来行列式是多少阶的。由上面这种形式展现,是可以看出它是n阶的。
例:写出四阶行列式中含有因子$a_{11}a_{23}$的项。
解:四阶行列式,那么每一项是不是应该取自不同行不同列呢?已经取完第一行第二行了,接下来应该取第几行?第三行第四行。所以行标应该是3、4,列标由于$a_{11}a_{23}$列标已经取完1、3。那列标还应该取什么呢?2、4或者4、2。所以它应该有这么两项。
$a_{11}a_{23}a_{34}a_{42}$,行标取1、2、3、4,列标已经有了1、3,可以写个4、2,再写个2、4。所以一定会取:$a_{11}a_{23}a_{34}a_{42}$、$a_{11}a_{23}a_{32}a_{44}$ 这两项,那么这两项的符号怎么来定呢?因为我们已经把行标写成标准次数,因此就由列标的逆序数来确定就可以。
因此$a_{11}a_{23}a_{34}a_{42}$的列标的逆序数为:$N(1342)=2$,偶数的符号为正
$a_{11}a_{23}a_{32}a_{44}$的列标逆序数为$N(1324)=1$,奇数的符号为负。所以综上所述四阶行列式中含有因子$a_{11}a_{23}$的项有两项:
$$ a_{11}a_{23}a_{34}a_{42}、-a_{11}a_{23}a_{32}a_{44} $$课堂练习:
【单选题】排列$a_{41}a_{52}a_{13}a_{34}a_{25}$的逆序数为()
N(45132)=7
A. 3
B. 7
C. 5
D. -7
正确答案:B
第四章 特殊行列式
4.1 上三角形行列式
主对角线以下全为零,主对角线以上有非零元素的,这种我们称为上三角行列式。
$$ \begin{align} D&=\begin{vmatrix} a_{11} & a_{12} & \cdots & a_{1n}\\ 0 & a_{22} & \cdots & a_{2n}\\ 0 & 0 & \ddots & \vdots \\ 0 & 0 & 0 & a_{nn} \\ \end{vmatrix}\\&=a_{11}a_{22}\cdots a_{nn} \end{align} $$由定义想一下,取自不同行不同列的$n$个元素的成绩。由于第一列只能取$a_{11}$,别的元素都是0,第一列取完了,第一行就不能取了,第二列,只能取$a_{22}$,以此类推,最后只能取到$a_{nn}$,我们发现上三角行列式是很好算的,就等于对角线元素的乘积。
4.2 下三角形行列式
主对角线以上全为零,主对角线以下有非零元素的,这种我们称为下三角行列式。
$$ \begin{align} D&=\begin{vmatrix} a_{11} & 0 & \cdots & 0\\ a_{21} & a_{22} & \cdots & 0\\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \\ \end{vmatrix}\\&=a_{11}a_{22}\cdots a_{nn} \end{align} $$它的结果也是对角线的元素乘积,和上三角行列式是类似的。
4.3 主对角行列式
只有主对角线的元素是非零元素,其余的元素全是零的行列式。
$$ \begin{align} D&=\begin{vmatrix} a_{11} & 0 & \cdots & 0\\ 0 & a_{22} & \cdots & 0\\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & a_{nn} \\ \end{vmatrix}\\&=a_{11}a_{22}\cdots a_{nn} \end{align} $$它是特殊的上三角行列式,也是特殊的下三角行列式,因此它的结果,等于对角线元素的乘积。
4.4 副对角行列式
从右上角到左下角的对角线的元素是非零元素,其余的元素全是零的行列式。
$$ \begin{align} D&=\begin{vmatrix} 0 & 0 & \cdots & 0 & a_{1n}\\ 0 & 0 & \cdots & a_{2,n-1} & 0\\ 0 & a_{n-1,2} & \ldots & 0 & \vdots \\ a_{n1} & 0 & \cdots & 0 \\ \end{vmatrix}\\&=(-1)^\frac{n(n-1)}{2}a_{1n}a_{2,n-1}\cdots a_{n1} \end{align} $$副对角线的结果是不是等于副对角线各个元素的乘积呢?事实上并不是。它前面应该带个符号。虽然行标写成标准次序了,但是列标的逆序数它不是标准排序,所以应该由列标$n(n-1)\cdots321$的逆序数$N(n(n-1)\cdots321)=\frac{n(n-1)}{2}$来确定前面的符号。所以副对角行列式的结果是前面是带符号的。
关于n阶行列式还有一个等价的定义。
我们给定义的时候,行标写成标准次序1到n。列标$j_1$到$j_n$是$1$到$n$的某个排列,一共是$n!$项。我们说由列标的逆序数的奇偶性$t=N(j_1j_2 \cdots j_n)$来确定它每个元的符号。这个是行标写成标准次序的时候。
$$ \begin{align} \begin{vmatrix} a_{11} & a_{12} & \cdots & a_{1n}\\ a_{21} & a_{22} & \cdots & a_{2n}\\ \vdots & \vdots & \vdots & \vdots\\ a_{n1} & a_{n2} & \cdots & a_{nn} \end{vmatrix}&= \sum(-1)^ta_{1j_i}a_{2j_2} \cdots a_{nj_n},t=N(j_1j_2\cdots j_n) \end{align} $$有同学自然要问了,如果是列标写成标准次序呢?可不可以由行标的逆序数,它的奇偶性来确定符号呢?是可以的,这是一个等价的定义。
$$ \begin{vmatrix} a_{11} & a_{12} & \cdots & a_{1n}\\ a_{21} & a_{22} & \cdots & a_{2n}\\ \vdots & \vdots & \vdots & \vdots\\ a_{n1} & a_{n2} & \cdots & a_{nn} \end{vmatrix}= \begin{align*} \sum(-1)^{t_1}a_{i_11}a_{i_22}\cdots a_{i_nn} \end{align*},t_1=N(i_1i_2\cdots i_n) $$注意:列标是从$1$到$n$写成标准次序。由行标 $i_1$ 到 $i_n$ 由它的逆序数的奇偶性来确定每项前面的符号。这是行标。
有的同学可能会问,如果有的公式,行标和列标都不是标准次序的呢?我们也有一个等价的公式。
$$ \begin{aligned} \begin{vmatrix} a_{11} & a_{12} & \cdots & a_{1n}\\ a_{21} & a_{22} & \cdots & a_{2n}\\ \vdots & \vdots & \vdots & \vdots\\ a_{n1} & a_{n2} & \cdots & a_{nn} \end{vmatrix}=& \sum(-1)^{t_2}a_{i_1j_1}a_{i_2j_2}\cdots a_{i_nj_n},t_2 \\&=N(i_1i_2\cdots i_n)+N(j_ij_2 \cdots j_n) \end{aligned} $$这里面的$t_2$就等于什么呢?行标的逆序数再加上列标的逆序数,它俩和的奇偶性来确定每一项的符号。
n阶行列式算的时候,行标写成标准次序,由列标来定,列标写成标准次序,由行标来定。如果是混的,那么由行标和列标逆序数和的奇偶性来确定它前面的符号。
例:由定义计算四阶行列式。
$$ D=\begin{vmatrix}a&0&0&b\\0&c&d&0\\0&e&f&0\\g&0&0&h\end{vmatrix} $$按照定义,是不是取自不同行不同列的乘积?主对角线$acfh$,一定会有这四项元素的乘积。那么我们取行的时候,第一行取 $a$ 、第二行取 $c$ 、第三行取 $f$ 、第四行取 $h$ ,都是从小到大取。
我们看一下它们的列标,用它们列标逆序数来确定它前面的符号。那么列的话,$a$ 是处于第一列,$c$ 处于第二列,$f$ 处于第三列,$h$ 处于第四列。因此我们可以算一下 $1234$ 的逆序数$N(1234)=0$ ,结果是偶数,所以它前面的符号是正号。
类似的我们取一下副对角线 $bdeg$ ,先取第一行、再取第二行、再取第三行、再取第四行。从小到大取,取完之后,看一下列标,$b$ 处于第四列,$d$ 处于第三列,$e$ 处于第二列,$g$ 处于第一列。因此 $N(4321)=6$ 是偶数,因此这一项是正号。
我们取完了吗?没有取完,再取一下,不同行不同列,第一行如果取 $a$ 的话,第二行不能取 $c$ ,因为 $c$ 已经取过了,再取应该取 $d$ 了。按照定义,取自不同行不同列,$ad$ 已经取完第一列和第三列了,接下来应该取第二列和第四列了。那剩下的只有$e$、$h$,所以应该加上$adeh$,那么它前面的符号怎么定呢?行标已经写成标准次序了,就看看 $adeh$ 所在的列,那就相当于第几列?$1324$,算出来的逆序数为:$N(1324)=1$,是奇数,符号取负号。
类似的,第一行取 $b$ 的话,第二行就不能取 $d$ 了,因为 $bd$ 已经取过了。那我们就应该取$c$ ,那第四列、第二列取完了,剩下就取第一列和第三列。那么剩下的也就是 $f$、$g$。所以就应该加上 $bcfg$,那么它的符号怎么定?行标已经写成标准次序了,看列标的逆序数就应该是 $N(4231)=5$ ,为奇数,符号取负号。
那么本题的四阶行列式由定义计算,结果为:
$$ D=acfh+bdeg-adeh-bcfg $$稍微复杂一点。后面计算高阶行列式还有别的方法。这个例子就是告诉大家,由定义来计算高阶行列式是怎么算的。
课堂练习:
【单选题】计算$D=\begin{vmatrix}a_1 & -a_1 & 0 & 0 \\ 0 & a_2 & -a_2 & 0 \\ 0 & 0 & a_3 & -a_3 \\ 1 & 1 & 1 & 1\end{vmatrix}$的值为()
A. $-a_1a_2a_3$
B. $a_1a_2a_3$
C. $4a_1a_2a_3$
D. $-4a_1a_2a_3$
正确答案:C
练习:
用四阶行列式定义来计算
$$ D_4=\begin{vmatrix} 0 & 0 & 0 & 1 \\ 0 & 0 & 2 & 0 \\ 0 & 3 & 0 & 0\\ 4 & 0 & 0 & 0 \end{vmatrix} $$用n阶行列式定义来计算
$$ D_n=\begin{vmatrix} 0 & 0 & \cdots & 0 & 1 & 0 \\ 0 & 0 & \cdots & 2 & 0 & 0 \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ n-1 & 0 & \cdots & 0 & 0 & 0 \\ 0 & 0 & \cdots & 0 & 0 & n \\ \end{vmatrix} $$第五章、行列式性质
5.1 行列式性质1、2
定义:$D$经过”行列互换”变为转置行列式$D^t$(Transposed determinant)。
$$ 设D=\begin{vmatrix} a_{11} & a_{12} & \cdots & a_{1n}\\ a_{21} & a_{22} & \cdots & a_{2n}\\ \vdots & \vdots & \vdots & \vdots\\ a_{n1} & a_{n2} & \cdots & a_{nn}\\ \end{vmatrix},则D^T=\begin{vmatrix} a_{11} & a_{21} & \cdots & a_{n1}\\ a_{12} & a_{22} & \cdots & a_{n2}\\ \vdots & \vdots & \vdots & \vdots\\ a_{1n} & a_{2n} & \cdots & a_{nn}\\ \end{vmatrix} $$行换成同序数的列,意思就是说,$D$的第一行在转置里面的第一列,类似的$D$的第二行在转置里面就变成第二列,以此类推,第$n$行就变成了第$n$列。也就相当于$D$的转置的代表元变成了$a_{ji}$,行列互换。
5.1.1 性质1
性质1:行列式与它的转置行列式相等。
$$ D^T=D $$证明:设$D=\begin{vmatrix}a_{ij}\end{vmatrix}$,$D^T=\begin{vmatrix}b_{ij}\end{vmatrix}$。
则$b_{ij}=a_{ji}(i,j=1,2,\cdots,n)$,回忆一下行列式的等价定义
如果行标写成标准次序 $1$ 到 $n$ 的话,这个 $t$ 就由列标的逆序数奇偶性来定。
或者是列标写成标准次序 $1$ 到 $n$ 的话,这个 $t$ 就由行标的逆序数奇偶性来定。
逆序数是奇数的取负号,逆序数是偶数的取正号。这是行列式的定义。
那么$D^T$的代表元是$b_{ij}$
则
$$ b_{ij}=a_{ji}(i,j=1,2,\cdots,n) $$ $$ \begin{align} D &= \sum(-1)^ta_{1j_1}a_{2j_2}\cdots a_{nj_n} \\&= \sum(-1)^ta_{j_11}a_{j_12} \cdots a_{j_nn},t=N(j_1 j_2 \cdots j_n) \end{align} $$ $D^T$由行列式的定义 $$ \begin{align} D^T &= \sum(-1)^tb_{1j_1}b_{2j_2} \cdots b_{nj_n}\\ &= \sum(-1)^ta_{j_11}a_{j_22} \cdots a_{j_nn}=D,t=N(j_1 j_2 \cdots j_n) \end{align} $$这个 $t$ 和上面的是一样的,相当于是列标 $j_1$ 到 $j_n$ 的逆序数。那么由$b_{ij}=a_{ji}$ 那么 $D^T$ 可以接着写,将所有的 $b$ 换成 $a$。
可以写成$\sum(-1)^ta_{j_11}a_{j_22} \cdots a_{j_nn}$就是行列式$D$
列标写成标准次序由行标的逆序数的奇偶性来确定符号的等价的定义。
所以我们就证出了,行列式的转置和原来的行列式相等的。
那转置行列式和原来的行列式相等说明什么呢?说明 $D^T=D$ 行和列在计算的时候具有相同的地位。
因为 $D$ 是取自不同行跟不同列的各个元素的乘积,
那 $D^T$ 就相当于不同列跟不同行的各个元素的乘积。
所以说行和列在计算的时候具有相同的地位。
5.1.2 性质2
性质2:互换行列式两行(列),行列式变号。
新的行列式记成$D'$与原来的行列式差一个符号,也就是
$$ D'=-D $$这是行列式的很重要的”运算性质”
互换$i$,$j$两行:$r_i \leftrightarrow r_j$,行用 $row$ 来表示,所以通常我们用第一个字母$r$来表示行。
互换$i$,$j$两列:$c_i\leftrightarrow c_j$,列用 $column$ 来表示,所以通常我们用第一个字母 $c$ 来表示列。
证明:设$D=\begin{vmatrix}a_{ij}\end{vmatrix}$,$D'=\begin{vmatrix}b_{ij}\end{vmatrix}$,其中$D’$由$D$互换$i$,$j$两行得到。
即当 $k\neq i,j$,$b_{kp} = a_{kp}$ ;$k$为行标,$p$为列标。
当$k=i,j$,$b_{ip}=a_{jp},b_{jp}=a_{ip}$;
要证明$D'=-D$
由定义得到:
$$ \begin{align} D'&=\sum(-1)^tb_{1p_1} \cdots b_{ip_i} \cdots b_{jp_j}\cdots b_{np_n} ① \\&=\sum(-1)^ta_{1p1} \cdots a_{jp_i} \cdots a_{ip_j} \cdots a_{np_n} ② \\&=\sum(-1)^ta_{1p1} \cdots a_{ip_j} \cdots a_{jp_i} \cdots a_{np_n}(因子乘积互换)③ \end{align} $$①、②式中的 $t=N(p_1 \cdots p_i \cdots p_j \cdots p_n)$ ,③式中的$t_1=N(p_1 \cdots p_j \cdots p_i \cdots p_n)$
可以发现上式①、② $b_{ip_i}$换成了$a_{jp_i}$。$b_{jp_i}$换成$a_{ip_i}$,行标换,列标不变,剩下的$b_{np_n}$换成$a_{np_n}$。所有的$b$换成了$a$。
注意:这个式子的行标不是标准次序。但是中间都是乘积项,那我换中间的第$i$项和第$j$项就是因子的乘积互换。经过因子乘积互换之后得到③,③可以保证行标是标准顺序。
注意这里的$t_1$与$t$的区别,是不是就相当于第 $i$ 个数 $p_i$ 和第 $j$ 个数 $p_j$ 它俩之间互换。那么它们两个的奇偶性正好相反,所以就有
$$ (-1)^t=-(-1)^{t_1} $$因为③式中的$t$
$$ t_1=N(p_1 \cdots p_j \cdots p_i \cdots p_n) $$所以
$$ D'=-\sum(-1)^{t_1}a_{1p_1} \cdots a_{ip_j} \cdots a_{jp_i} \cdots a_{np_n}=-D(由定义) $$这个列标的逆序数恰好是$t_1$,可以分析,如果把sigma前面的负号去掉,是否恰好等于行列式$D$的定义?行标写成标准次序,由列标的逆序数来定它的符号。所以它等于$-D$。
综上,这样就证明互换行列式两行,行列式改变符号。类似的互换行列式的两列,行列式也改变符号。记住结论:换行就变号。
例:$\begin{vmatrix}1&2&3\\1&0&-1\\0&1&1\end{vmatrix} {r_1 \leftrightarrow r_3} -\begin{vmatrix}0&1&1\\-1&0&-1\\1&2&3\end{vmatrix}$
前面的行列式换第一行和第三行,记成$r_1$、$r_3$互换,因为由性质2可知,互换之后肯定要改变符号,所以右侧变为负数。
推论:若行列式有两行(列)相同,则行列式的值为0。
为什么?有两行相同,那么互换两行只是改变符号,但这两行还是一样的,那换行之后跟原来的相等。那是不是相当于$x=-x$,那$x=0$,所以一个行列式如果有两行或两列相同,它的值都是0。
例:$\begin{vmatrix}1&2&3\\1&0&-1\\1&2&3\end{vmatrix} r_1 \leftrightarrow r_3 -\begin{vmatrix}1&2&3\\1&0&-1\\1&2&3\end{vmatrix}$
第一行和第三行经过互换之后,改变符号,相当于$D=-D$,所以
$$ \begin{vmatrix}1&2&3\\1&0&-1\\1&2&3\end{vmatrix} r_1 \leftrightarrow r_3 -\begin{vmatrix}1&2&3\\1&0&-1\\1&2&3\end{vmatrix}=0 $$课堂练习
【判断题】 行列式$\begin{vmatrix}1 & 2 & 3\\ 1 & 0 & -1 \\ 3 & 6 & 9\end{vmatrix}$等于0。
A. 对
B. 错
正确答案:A
5.2 行列式性质3、4、5
5.2.1 性质3
用非零数 $k$ 乘行列式的某一行(列)所有元素,等于用数$k$乘以此行列式。
$$ D'=kD $$因为行列式的定义是取不同行,不同列的 $n$ 个元素的乘积。
用 $k$ 乘第 $i$ 行:每一项的第$i$行是不是都出现了$k$倍。那么 $k$ 是可以提出来,所以
$$ r_i \times k $$用$k$乘第$i$列:每一项的第$i$列是不是都出现了$k$倍。那么$k$同样也是可以提出来的,所以
$$ c_i \times k $$例:
$$ \begin{vmatrix}1 & 2 & 3\\1 & 0 & -1\\1 & 1 & 1\end{vmatrix}r_1\times 2 \begin{vmatrix}2 & 4 & 6\\1 & 0 & -1\\0 & 1 & 1\end{vmatrix} $$那么右侧的第一行变成了 $246$ ,与左侧的第一行查了两倍。并且这个 $2$ 是可以提出来的。
推论:行列式中某一行(列)的公因子可提到行列式符号外面。
例子:
$$ \begin{vmatrix}2 & 4 & 6\\1 & 0 & -1\\0 & 1 & 1\end{vmatrix}= 2\begin{vmatrix}1 & 2 & 3\\1 & 0 & -1\\0 & 1 & 1\end{vmatrix} $$推论:若行列式有两行(列)的对应元素成比例,则行列式等于0。
若行列式有两行(列)的对应元素成比例,我们说由刚才的性质,这个常数 $k$ 可以提出去。提出去后,这两行对应相等。根据 性质2 的推论,行列式中有两行相等,则行列式的值为0。
例:
$$ \begin{vmatrix}-2 & -4 & -6\\1 & 0 & -1\\1 & 2 & 3\end{vmatrix}=-2 \begin{vmatrix}1 & 2 & 3\\1 & 0 & -1\\1 & 2 & 3\end{vmatrix}=0 $$可以观察上式的左侧,第一行和第三行差$-2$倍,那么我们把第一行提出公因子$-2$,得到中间的行列式,又由于第一行和第三行相同,因此根据性质2 的推论,行列式中有两行相等,则行列式的值为0,所以最终结果为0。
5.2.2 性质4
性质4:若行列式某一行是两组数的和,则此行列式就等于如下两行列式的和。
$$ \begin{vmatrix} a_{11} & \cdots & a_{1n}\\ \vdots & & \vdots\\ b_{i1}+c_{i1} & \cdots & b_{in}+c_{in}\\ \vdots & & \vdots\\ a_{n1} & \cdots & a_{nn} \end{vmatrix} = \begin{vmatrix} a_{11} & \cdots & a_{1n}\\ \vdots & & \vdots\\ b_{i1} & \cdots & b_{in}\\ \vdots & & \vdots\\ a_{n1} & \cdots & a_{nn} \end{vmatrix} + \begin{vmatrix} a_{11} & \cdots & a_{1n}\\ \vdots & & \vdots\\ c_{i1} & \cdots & c_{in}\\ \vdots & & \vdots\\ a_{n1} & \cdots & a_{nn} \end{vmatrix} $$左侧行列式中加号左侧的第$i$行,可以写成右侧的第一个行列式。
左侧行列式中加号左侧的第$i$行,可以写成右侧的第二个行列式。
也就是说
$$ D'=D_1+D_2 $$例:
$$ \begin{vmatrix} 1+0 & 1+1 & 1+2\\ 1 & 0 & -1\\ 0 & 1 & 1 \end{vmatrix} = \begin{vmatrix} 1 & 1 & 1\\ 1 & 0 & -1\\ 0 & 1 & 1 \end{vmatrix} + \begin{vmatrix} 0 & 1 & 2\\ 1 & 0 & -1\\ 0 & 1 & 1 \end{vmatrix} $$课堂练习:
【判断题】计算行列式
$$ \begin{vmatrix} 1+0 & 0+1 & -1+1\\ 1 & 0 & -1\\ 0 & 1 & 1 \end{vmatrix} = \begin{vmatrix} 1 & 0 & -1\\ 1 & 0 & -1\\ 0 & 1 & 1 \end{vmatrix} + \begin{vmatrix} 0 & 1 & 1\\ 1 & 0 & -1\\ 0 & 1 & 1 \end{vmatrix} =0 $$A. 对
B. 错
正确答案:A
5.2.3 性质5
性质5:行列式的某一行(列)的所有元素乘以同一数$k$后再加到另一行(列)对应的元素上去,行列式的值不变。
也就是说
$$ D'=D $$ $$ \begin{align} \begin{vmatrix} a_{11} & \cdots & a_{1n}\\ \vdots & & \vdots \\ a_{i1}+ka_{j1} & \cdots & a_{in}+ka_{jn}\\ \vdots & & \vdots \\ a_{j1} & \cdots & a_{jn}\\ \vdots & & \vdots \\ a_{n1} & \cdots & a_{nn} \end{vmatrix} &= \begin{vmatrix} a_{11} & \cdots & a_{1n}\\ \vdots & & \vdots \\ a_{i1} & \cdots & a_{in}\\ \vdots & & \vdots \\ a_{j1} & \cdots & a_{jn}\\ \vdots & & \vdots \\ a_{n1} & \cdots & a_{nn} \end{vmatrix} + \begin{vmatrix} a_{11} & \cdots & a_{1n}\\ \vdots & & \vdots \\ ka_{j1} & \cdots & ka_{jn}\\ \vdots & & \vdots \\ a_{j1} & \cdots & a_{jn}\\ \vdots & & \vdots \\ a_{n1} & \cdots & a_{nn} \end{vmatrix}\\ &= \begin{vmatrix} a_{11} & \cdots & a_{1n}\\ \vdots & & \vdots \\ a_{i1} & \cdots & a_{in}\\ \vdots & & \vdots \\ a_{j1} & \cdots & a_{jn}\\ \vdots & & \vdots \\ a_{n1} & \cdots & a_{nn} \end{vmatrix} \end{align} $$根据性质3,$\begin{vmatrix}
a_{11} & \cdots & a_{1n}\
\vdots & & \vdots \
ka_{j1} & \cdots & ka_{jn}\
\vdots & & \vdots \
a_{j1} & \cdots & a_{jn}\
\vdots & & \vdots \
a_{n1} & \cdots & a_{nn}
\end{vmatrix}$可以公因子$k$提到外面,又由于该行列式存在相同的行,因此结果为0。
因此:
用数$k$乘第$j$行加到第$i$行上:$r_i+k\times r_j$
用数$k$乘第$j$列加到第$i$列上:$c_i + k \times c_j$
例:
$$ \begin{vmatrix} 1 & 2 & 3\\ 1 & 0 & -1\\ 0 & 1 & 1 \end{vmatrix} {r_2-r_1} \begin{vmatrix} 1 & 2 & 3\\ 0 & -2 & -4\\ 0 & 1 & 1 \end{vmatrix} $$解:即左边的行列式的第一行乘以$k=1$,得$1 2 3$,加上左边的行列式的第二行,因此结果是
$$ \begin{align} \begin{vmatrix} 1 & 2 & 3\\ 1 & 0 & -1\\ 0 & 1 & 1 \end{vmatrix} &= \begin{vmatrix} 1 & 2 & 3\\ 1 + (1 \times k) & 0 + (2 \times k) & -1 + (3 \times k)\\ 0 & 1 & 1 \end{vmatrix} \\&= \begin{vmatrix} 1 & 2 & 3\\ 0 & -2 & -4\\ 0 & 1 & 1 \end{vmatrix} ,k=1 \end{align} $$5.2.4 小结
行列式性质:
- $r_i \leftrightarrow r_j(c_i \leftrightarrow c_j)$ $D'=-D$,互换两行或两列,则改变符号。
- $r_i \times (c_i \times k)$ $D'=kD$,某一行或某一列乘上常数$k$,相当于多一个$k$倍,新得的行列式等于$kD$。
- $r_i+kr_j(c_i+kc_j)$ $D'=D$,某一行或某一列的$k$倍加到另外一行或另外一列上面去,行列式的值不变。
其它性质:
转置行列式与原来行列式相等。
$$ D^T=D $$某一行可以拆成两部分的话,新的行列式等于两部分行列式的和。
$$ D'=D_1+D_2 $$5.3 行列式性质的应用
思想是把它化成上三角行列式或下三角行列式。因为三角行列式好算,它就等于对角线元素的乘积。
例:计算
$$ D=\begin{vmatrix} 1 & 1 & -1 & 2\\ -1 & -1 & -4 & 1\\ 2 & 4 & -6 & 1\\ 1 & 2 & 2 & 2 \end{vmatrix} $$解:若想将上式化为上三角行列式的话,那么对角线的左下角就应该化成0。
第二行第一个元素是$-1$,化成$0$,可以将第一行加到第二行上面去,是不是就是相当于第一行的一倍加到第二行上面去,由行列式的性质,值是否不变?
第三行的$2$若要化成$0$,则第一行乘以$-2$,加到第三行上去。
类似的,
第四行的$1$若要化成$0$,则第一行乘以$-1$,加到第四行上去。
就相当于$r_4-r_1$,就可以把行列式的第二、第三、第四行的第一列都化成0。
$$ D=\begin{vmatrix} 1 & 1 & -1 & 2\\ -1 & -1 & -4 & 1\\ 2 & 4 & -6 & 1\\ 1 & 2 & 2 & 2 \end{vmatrix} \begin{align} { r_2+r_1\\ r_3-2r_1\\ r_4-r_1 } \end{align} \begin{vmatrix} 1 & 1 & -1 & 2\\ 0 & 0 & -5 & 3\\ 0 & 2 & -4 & -3\\ 0 & 1 & 3 & 0 \end{vmatrix} $$接下来就处理右下角的三阶行列式 $$\begin{vmatrix}0 & -5 & 3\\2 & -4 & -3\\1 & 3 & 0\end{vmatrix}$$,想办法把这个行列式化为上三角行列式。想化为上三角行列式,对角线上的元素应该是常数。那就相当于$D$的第二行第二列化成$1$,因此,我们可以将第一行和第四行,调换一下位置,因为互换了第二行和第四行,因此符号变成负。
$$ r_2 \leftrightarrow r_4 -\begin{vmatrix} 1 & 1 & -1 & 2\\ 0 & 1 & 3 & 0\\ 0 & 2 & -4 & -3\\ 0 & 0 & -5 & 3 \end{vmatrix} $$接下来,需要将第三行第二列中的$2$化成$0$?可以用第三行减去第二行的两倍。
$$ r_2 \leftrightarrow r_4 -\begin{vmatrix} 1 & 1 & -1 & 2\\ 0 & 1 & 3 & 0\\ 0 & 2 & -4 & -3\\ 0 & 0 & -5 & 3 \end{vmatrix}r_3-2r_2- \begin{vmatrix} 1 & 1 & -1 & 2\\ 0 & 1 & 5 & 0\\ 0 & 0 & -10 & -3\\ 0 & 0 & -5 & 3 \end{vmatrix} $$接下来,再观察右下角$\begin{vmatrix}-10 & -3\\-5 & 3\end{vmatrix}$,这么把该行列式化成上三角行列式呢?可以观察到右下角行列式第一行第一列为$-10$,我们尽可能让主对角元素变成是小的。因此我们可以对第三行和第四行换一下位置,因为互换了第三行和第四行,因此符号变成正号。
$$ -\begin{vmatrix} 1 & 1 & -1 & 2\\ 0 & 1 & 5 & 0\\ 0 & 0 & -10 & -3\\ 0 & 0 & -5 & 3 \end{vmatrix} r_3{\leftrightarrow}r_4 \begin{vmatrix} 1 & 1 & -1 & 2\\ 0 & 1 & 5 & 0\\ 0 & 0 & -5 & 3\\ 0 & 0 & -10 & -3 \end{vmatrix} $$接下来,再观察$\begin{vmatrix}-5&3\\-10&-3\end{vmatrix}$,我们把 $-10$ 化成 $0$ 就可以了,也就是用第三行乘以$-2$,再加上第四行:
$$ \begin{vmatrix} 1 & 1 & -1 & 2\\ 0 & 1 & 5 & 0\\ 0 & 0 & -5 & 3\\ 0 & 0 & -10 & -3 \end{vmatrix} r_4-2r_3 \begin{vmatrix} 1 & 1 & -1 & 2\\ 0 & 1 & 5 & 0\\ 0 & 0 & -5 & 3\\ 0 & 0 & 0 & -9 \end{vmatrix} $$最终,我们得到一个上三角行列式。上三角行列式的结果,等于对角线元素的成绩
$$ 1 \times 1 \times (-5) \times -9 = 45 $$应用行列式的性质计算行列式,我们的思想就是想办法,将行列式化成上三角行列式,或者下三角行列式。计算的时候,就会非常方便。
课堂练习:
【单选题】计算行列式$\begin{vmatrix}1 & 2 & 3 & 4\\1 & 0 & 1 & 2\\3 & -1 & -1 & 0\\1 & 2 & 0 & -5\end{vmatrix}$的值为()
A. 24
B. -24
C.12
D.-4
正确答案:B
例:计算$D=\begin{vmatrix}3 & 1 & 1 & 1 \\1 & 3 & 1 & 1 \\1 & 1 & 3 & 1 \\1 & 1 & 1 & 3\end{vmatrix}$
观察其特点,这样的行列式,每行或者每列都加到同一行,或同一列上面去。发现它们的和都一样(每一行横向和或每一列的纵向和),都是$6$,所以这种行列式,我们叫”行等和”行列式。所以在计算它的时候,我们是有技巧的。
解:
将除第一列的其它列加到第一列去。
$$ D=\begin{vmatrix} 6 & 1 & 1 & 1\\ 6 & 3 & 1 & 1\\ 6 & 1 & 3 & 1\\ 6 & 1 & 1 & 3 \end{vmatrix} $$我们说,某一行或某一列有公因子,可以提到外面。因此,我们可以把$6$提出来,变成
$$ D=\begin{vmatrix} 6 & 1 & 1 & 1\\ 6 & 3 & 1 & 1\\ 6 & 1 & 3 & 1\\ 6 & 1 & 1 & 3 \end{vmatrix} =6\begin{vmatrix} 1 & 1 & 1 & 1\\ 1 & 3 & 1 & 1\\ 1 & 1 & 3 & 1\\ 1 & 1 & 1 & 3 \end{vmatrix} $$各行同时减去第一行
$$ =6\begin{vmatrix} 1 & 1 & 1 & 1\\ 1 & 3 & 1 & 1\\ 1 & 1 & 3 & 1\\ 1 & 1 & 1 & 3 \end{vmatrix} = 6 \begin{vmatrix} 1 & 1 & 1 & 1\\ 0 & 2 & 0 & 0\\ 0 & 0 & 2 & 0\\ 0 & 0 & 0 & 2 \end{vmatrix} $$那么原来对角线左下角凡是$1$的值,都变成了$0$。观察可看到,现在变成了上三角行列式。
那么上三角行列式的是不是就等于对角线的乘积,再乘以前面的6?
因此结果为:
$$ 6\times1\times2\times2\times2=48 $$一般”行等和”行列式,都是这么计算的。