实验：机器学习之K-Means聚类
2024-09-11 16:03:49 #人工智能 #机器学习 #无监督学习

实验：机器学习之 K-Means 聚类

第一章 K-Means 介绍

第一节 什么是 K 均值聚类

如今人工智能发展迅速，有许多用于“聚类”的模型。在这个课程中，我们将展示被认为是其中最简单的模型之一：K-Means 聚类。尽管“K-Means”很简单，但它仍然在许多数据科学应用中被广泛用。

无监督机器学习是一个过程，即教导计算机运用未标记、未分类的数据，使算法能在无监督情况下对这些数据进行操作。在没有先前数据训练的情况下，机器的任务就是依据相似性、模式和变化来整理未排序的数据。

K 代表聚类，它依据数据点与聚类中心的距离，将数据点分配到 K 个聚类中的一个。它首先会在空间中随机设定簇质心，然后每个数据点根据与簇质心的距离分配到相应的簇。在将每个点分配到某个簇后，会重新设定簇质心。此过程不断迭代，直至找到良好的集群。在分析中，假定簇的数量是预先给定的，且必须将点归入其中一组。

在某些情形下，K 没有明确界定，我们需考虑 K 的最佳数量。K 意味着聚类表现最佳，数据能很好地分离。当数据点重叠时，该聚类不适用。与其他聚类技术相比，K 均值聚类速度更快，提供了数据点之间的强耦合。但 K 均值聚类不能提供明确的聚类质量信息，不同的簇质心初始分配可能导致不同的簇。此外，K 均值算法对噪声敏感，可能陷入局部最小值。

K-Means 应用案例：

  • 客户细分
  • 了解网站访问者试图完成什么
  • 模式识别
  • 机器学习
  • 数据压缩

第二节 k 均值聚类的目标是什么

聚类的目标在于把总体或数据点集划分成多个组，使得每个组内的数据点相互间更具可比性，同时与其他组内的数据点存在差异。其本质就是依据事物间相似程度与不同程度来对事物进行分组。

第三节 k 均值聚类的工作原理

我们获取一组具有特定特征及对应值（如向量形式）的项目数据集，任务是对这些项目进行分类。为此，我们采用 K-means 算法，这是一种无监督学习算法，其中的“K”代表要将项目分类成的组或簇的数量。（可将项目视作 n 维空间中的点来理解）。该算法会把项目分成 k 个相似的组或簇，计算相似度时采用欧几里得距离作为度量标准。

其具体工作流程如下：
首先，随机初始化 k 个点，称之为均值或聚类质心。然后，将每个项目归类到距离其最近的均值所属的类别，并更新均值的坐标，使其成为该簇中已分类项目的平均值。重复该过程特定的迭代次数后，便得到最终的簇。上述所提到的“点”被称作均值，是因为它们是所在分类项目的平均值。对于初始化这些均值，我们有多种选择，一种较为直观的方法是用数据集中随机项目的均值来初始化，另一种方法是在数据集边界范围内的随机值处初始化均值（若对于特征 x，项目的值处于[0,3]区间内，就用[0,3]内的 x 值来初始化均值）。

K-Means 伪代码：

1
2
3
4
5
6
7
8
初始化 k 个均值为随机值
重复以下步骤指定的迭代次数：
    遍历所有项目：
        计算项目与每个均值的欧几里得距离
        确定最接近项目的均值
        将项目分配给该均值
    对于每个簇：
        通过计算簇中项目的平均值来更新该簇的均值

第二章 实验部分

第一节 安装环境

1
pip install seaborn pandas numpy matplotlib

第二节 K-Means 聚类实验（纯代码实现）

make_blobs函数是sklearn.datasets中的一个函数，主要用于产生聚类数据集，生成一个数据集和相应的标签。以下是make_blobs函数的参数说明：

  • n_samples：表示数据样本点个数，默认值为 100。
  • n_features：表示每个样本的特征（或属性）数，也表示数据的维度，默认值为 2。
  • centers：表示类别数（标签的种类数），默认值为 3。
  • cluster_std：表示每个类别的方差，浮点数或者浮点数序列，默认值为 1.0。例如，若希望生成 2 类数据，其中一类比另一类具有更大的方差，可以将cluster_std设置为浮点数 1.0~3.0。
  • center_box：中心确定之后的数据边界，默认值为(-10.0,10.0)。
  • shuffle：将数据进行洗乱，默认值是True。
  • random_state：官网解释是随机生成器的种子，可以固定生成的数据。给定数之后，每次生成的数据集就是固定的。若不给定值，则由于随机性将导致每次运行程序所获得的结果可能有所不同。在使用数据生成器练习机器学习算法练习或 python 练习时建议给定数值。

2.1 数据初始化

1
2
3
4
5
6
7
8
9
10
11
12
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs

# 生成聚类数据集
X,y = make_blobs(n_samples = 500, n_features = 2, centers = 3, random_state = 23)

# 绘制数据集的二维平面图
fig = plt.figure(0)
plt.grid(True)
plt.scatter(X[:,0], X[:,1])
plt.show()

2.2 初始化随机质心

代码为 K-means 聚类初始化三个聚类。它设置一个随机种子并在指定范围内生成随机簇中心，并为每个簇创建一个空的点列表。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
# 定义要划分的簇的数量
k = 3

# 创建空字典来存储簇的信息
clusters = {}

# 设置随机种子为固定值，使得每次实验的效果是一致的
np.random.seed(23)

# 按簇数量次数循环
for idx in range(k):
    # 生成在指定区间 (-2, 2) 内的随机向量来作为中心
	center = np.random.uniform(low=-2, high=2, size=X.shape[1])

    # 创建一个空列表来存储属于该簇的点
	points = []

    # 将 中心点和点列表 存储在clusters[idx]
	clusters[idx] = {
		'center' : center,
		'points' : []
	}

# 打印查看
clusters

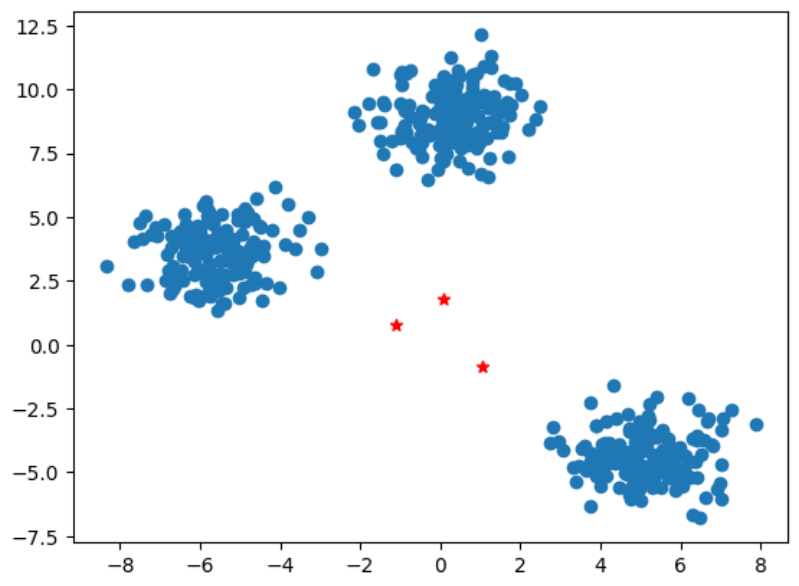
2.3 绘制中心点

该图以网格线显示数据点 $(X[:,0], X[:,1])$ 的散点图。它还标记了 K-means 聚类生成的初始聚类中心(红色星星)。

1
2
3
4
5
6
7
8
9
10
11
12
13
# 绘制随机生成的簇数据
plt.scatter(X[:,0], X[:,1])

# 显示网格
plt.grid(True)

# 用红色的星号形状，显示中心点位置
for i in clusters:
    center = clusters[i]['center']
    plt.scatter(center[0],center[1],marker = '*',c = 'red')

# 显示图片
plt.show()

2.4 定义欧几里得距离

欧几里得距离是一种在欧几里得空间中衡量两点之间距离的方法。
具体来说，对于空间中的两个点 $P(x_1,y_1,z_1,…)$ 和 $Q(x_2,y_2,z_2,…)$，它们之间的欧几里得距离就是各对应坐标分量差值的平方和的平方根，即：

$$
d(P,Q) = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2 + \cdots}
$$

它是一种非常基础且广泛应用的距离概念，在许多领域如数学、物理学、计算机科学等中都有重要作用，常用于聚类分析、模式识别等方面。

1
2
3
# 定义欧式距离
def distance(p1, p2):
	return np.sqrt(np.sum((p1 - p2) ** 2))

2.5 创建分配和更新集群中心的功能

E 步（Expectation 步）是根据当前的聚类中心，计算每个数据点属于每个聚类的概率。

在 K-Means 中，可以通过计算每个数据点到每个聚类中心的距离来确定概率。距离越近，数据点属于该聚类的概率就越高。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
# 实施E步
def assign_clusters(X, clusters):
    # 获取数据点的个数
    dots_num = X.shape[0]

    for idx in range(dots_num):
        # 创建一个距离列表
        dist = []

        # 获取数据点
        curr_x = X[idx]

        # 按簇数量个数进行循环
        for i in range(k):
            # 计算当前数据点与该簇中心的欧几里得距离
            dis = distance(curr_x, clusters[i]['center'])

            # 保存到距离列表
            dist.append(dis)

        # 找到距离列表中最小值的索引
        curr_cluster = np.argmin(dist)

        # 将当前数据点添加到该簇的点列表中
        clusters[curr_cluster]['points'].append(curr_x)

    # 返回簇
    return clusters

所以，E 步实际上找 一个蓝色的点 与 三个红色星星 对比距离，距离短的，就归属对应的红色星星所有。

1715793341382

M 步（Maximization 步）是根据 E 步计算出的概率，重新计算聚类中心。

在 K-Means 中，更新聚类中心的方法是将属于每个聚类的数据点的平均值作为新的聚类中心。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
# 实施M步
def update_clusters(X, clusters):
    # 按簇数量个数进行循环
    for i in range(k):
        # 将当前簇的所有点并转换为数组
        points = np.array(clusters[i]['points'])

        # 如果该簇有点（即点的数量大于 0）
        if points.shape[0] > 0:
            # 计算这些点在各个维度上的平均值作为新的簇中心
            new_center = points.mean(axis =0)

            # 并更新簇中心的值
            clusters[i]['center'] = new_center

            # 同时将该簇的点列表清空
            clusters[i]['points'] = []

    # 返回簇
    return clusters

所以，M 步事实上，平均 E 步所收集的点（将收集的点的 x 坐标累加在再平均，y 坐标累加再平均）得到一个新的中心点坐标。

2.6 创建用于预测数据点集群的函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
def pred_cluster(X, clusters):
    # pred列表 存储预测结果
    pred = []

    # 获取数据点的个数
    dots_num = X.shape[0]
    for i in range(dots_num):
        # 距离列表
        dist = []

        # 按簇数量循环
        for j in range(k):
            # 计算要 推理的数据点 与 每个簇中心点的距离
            d = distance(X[i], clusters[j]['center'])
            # 将距离收集起来
            dist.append(d)

        # 判断一下 推理的数据点 与 三个中心点 最近的结果，并且作为推理结果。
        pred.append(np.argmin(dist))

    # 返回推理结果
    return pred

2.7 赋值、更新中心点位置、推理

1
2
3
4
5
6
7
8
# E步：将蓝点分配给红星
clusters = assign_clusters(X, clusters)

# M步：不断更新红星在它所属的蓝星的位置
clusters = update_clusters(X, clusters)

# 推理
pred = pred_cluster(X, clusters)

2.8 显示推理结果

1
2
3
4
5
6
7
8
9
10
11
12
# 将原来的蓝点，按照推理的分类显示不同颜色
plt.scatter(X[:,0], X[:,1], c = pred)

# 显示簇
for i in clusters:
    # 质心
    center = clusters[i]['center']
    # 显示中心点
    plt.scatter(center[0], center[1], marker = '^', c = 'red')

# 显示图片
plt.show()

第三节 K-Means 聚类实验（sklearn 实现）

3.1 抑制警告

这段代码的主要作用是抑制（屏蔽）警告信息。
通过自定义一个名为 warn 的函数，它什么也不做（只是直接通过），然后将 warnings 模块中的 warn 方法替换为这个自定义的函数，这样当有警告产生时，就不会实际输出或显示这些警告信息了。

1
2
3
4
5
# 抑制警告
def warn(*args, **kwargs):
    pass
import warnings
warnings.warn = warn

3.2 数据初始化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
import random
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs

# 图像嵌入显示
%matplotlib inline

# 设置随机数种子
np.random.seed(0)

# 中心点
centers = [
    [4,4],
    [-2, -1],
    [2, -3],
    [1, 1]
]

# 生成中心点左边 X 和 分类y
X, y = make_blobs(n_samples=5000, centers=centers, cluster_std=0.9)

# 显示随机生成的聚类数据
plt.scatter(X[:, 0], X[:, 1], marker='.')

%matplotlib inline 主要的作用：在使用 Jupyter Notebook 等交互式环境时，它使得 matplotlib 绘制的图形可以直接嵌入在当前的 Notebook 页面内显示，而不是弹出单独的窗口来展示图形。这样方便在 Notebook 中直接查看和交互图形，有助于进行数据分析和可视化的过程。

3.3 设置 K-Means 函数

首先，我们进行 KMeans 设置。现在我们有了随机数据。

KMeans 类有很多可使用的参数，这里我们使用以下三个：

  • init（初始化质心的方法）：值为 "k-means++"，表示以一种智能的方式选择初始聚类中心来加速收敛。
  • n_clusters（要形成的簇的数量以及要生成的质心数量）：值为 4，因为我们有 4 个中心。
  • n_init 定义了要运行算法的次数，默认情况下，n_init 设置为 10，这意味着算法将在 10 个不同的随机初始质心上运行，并返回最佳结果。

然后，使用这些参数初始化 KMeans，将输出参数命名为 k_means。

1
2
3
4
5
# 设置参数
k_means = KMeans(init="k-means++", n_clusters=4, n_init=12)

# 训练
k_means.fit(X)

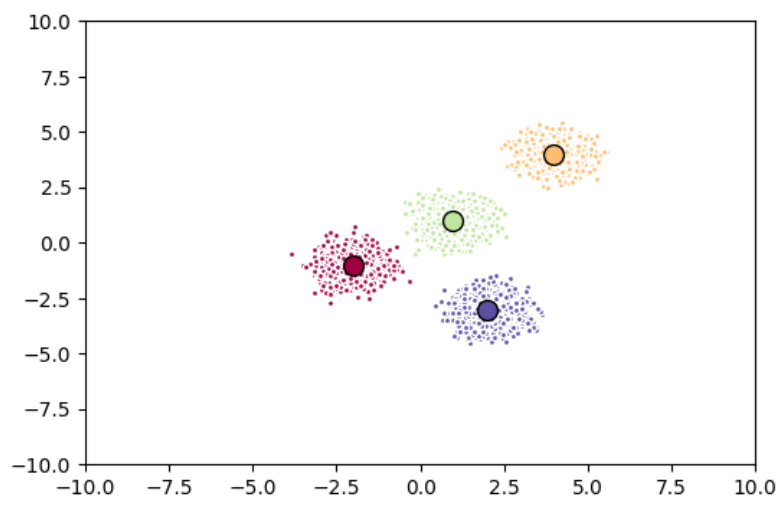
3.4 显示图像

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
# 创建一个图形对象，并设置其大小为宽6 高4
fig = plt.figure(figsize=(6, 4))

# 使用 plt.cm.Spectral 颜色映射来获取一系列颜色。
# 通过 np.linspace(0, 1, n_clusters)) 来生成一个在 0 到 1 之间均匀分布的序列。
colors = plt.cm.Spectral(np.linspace(0, 1, n_clusters))

# 在图形中添加一个子图
ax = fig.add_subplot(1, 1, 1)

plt.xlim(-10, 10)
plt.ylim(-10, 10)

for k, col in zip(range(n_clusters), colors):
    # 筛选出对应分类的点，
    my_members = (k_means3.labels_ == k)

    # 绘制属于该簇的成员点，点的颜色由当前颜色col确定，标记为小点。
    ax.plot(X[my_members, 0], X[my_members, 1], 'w', markerfacecolor=col, marker='.')

    # 获取当前簇的中心坐标
    cluster_center = k_means3.cluster_centers_[k]

    # 绘制簇中心，标记为圆形，颜色也是当前颜色，边缘为黑色，大小为10。
    ax.plot(cluster_center[0], cluster_center[1], 'o', markerfacecolor=col,  markeredgecolor='k', markersize=10)

# 显示图像
plt.show()

3.5 完整代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs

%matplotlib inline

np.random.seed(0)

# 中心点
centers = [
    [4,4],
    [-2, -1],
    [2, -3],
    [1, 1]
]

# 生成中心点左边 X 和 分类y
X, y = make_blobs(n_samples=5000, centers=centers, cluster_std=0.5)


# 实例化KMeans让其训练，初始化4个质点，让其训练到中央位置
n_clusters = 4
k_means3 = KMeans(init="k-means++", n_clusters=n_clusters, n_init=12)
k_means3.fit(X)

# 创建一个图形对象，并设置其大小为宽6 高4
fig = plt.figure(figsize=(6, 4))

# 使用 plt.cm.Spectral 颜色映射来获取一系列颜色。
# 通过 np.linspace(0, 1, n_clusters)) 来生成一个在 0 到 1 之间均匀分布的序列。
colors = plt.cm.Spectral(np.linspace(0, 1, n_clusters))

# 在图形中添加一个子图
ax = fig.add_subplot(1, 1, 1)

plt.xlim(-10, 10)
plt.ylim(-10, 10)

for k, col in zip(range(n_clusters), colors):
    # 筛选出对应分类的点，
    my_members = (k_means3.labels_ == k)

    # 绘制属于该簇的成员点，点的颜色由当前颜色col确定，标记为小点。
    ax.plot(X[my_members, 0], X[my_members, 1], 'w', markerfacecolor=col, marker='.')

    # 获取当前簇的中心坐标
    cluster_center = k_means3.cluster_centers_[k]

    # 绘制簇中心，标记为圆形，颜色也是当前颜色，边缘为黑色，大小为10。
    ax.plot(cluster_center[0], cluster_center[1], 'o', markerfacecolor=col,  markeredgecolor='k', markersize=10)

# 显示图像
plt.show()

1715797052317

第四节 K-Means 聚类鸢尾花分类实验（sklearn 实现）

img

4.1 加载鸢尾花数据

1
2
3
4
5
6
7
8
9
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
import matplotlib.cm as cm
from sklearn.datasets import load_iris
from sklearn.cluster import KMeans

X, y = load_iris(return_X_y=True)

4.2 找到最佳簇数

1
2
3
4
5
6
# 找到最佳簇数
sse = [] # 平方和误差
for k in range(1,11):
	km = KMeans(n_clusters=k, random_state=2)
	km.fit(X)
	sse.append(km.inertia_)

4.3 显示簇数与误差的关系

“Sum Squared Error”的意思是“误差平方和”或“平方误差总和”。
对于一组实际值 $y_i$ 和预测值 $\hat{y}_i$（$i=1,2,\cdots,n$），误差平方和的公式为：

$$
SSE = \sum_{i=1}^{n}(y_i - \hat{y}_i)^2
$$

它常被用于评估模型预测值与实际值之间的偏差程度。

1
2
3
4
5
6
7
8
sns.set_style("whitegrid")
g=sns.lineplot(x=range(1, 11), y=sse)

g.set(xlabel ="Number of cluster (k)",
	ylabel = "Sum Squared Error",
	title ='Elbow Method')

plt.show()

img

从上图中，我们可以观察到，在 k=2 和 k=3 时，肘状的情况。我们考虑 K=3。

4.4 构建 Kmeans 聚类模型

1
2
kmeans = KMeans(n_clusters=3, random_state=2)
kmeans.fit(X)

4.5 找到簇中心

1
kmeans.cluster_centers_

4.6 推理

1
2
pred = kmeans.fit_predict(X)
pred

4.7 输出图像

img

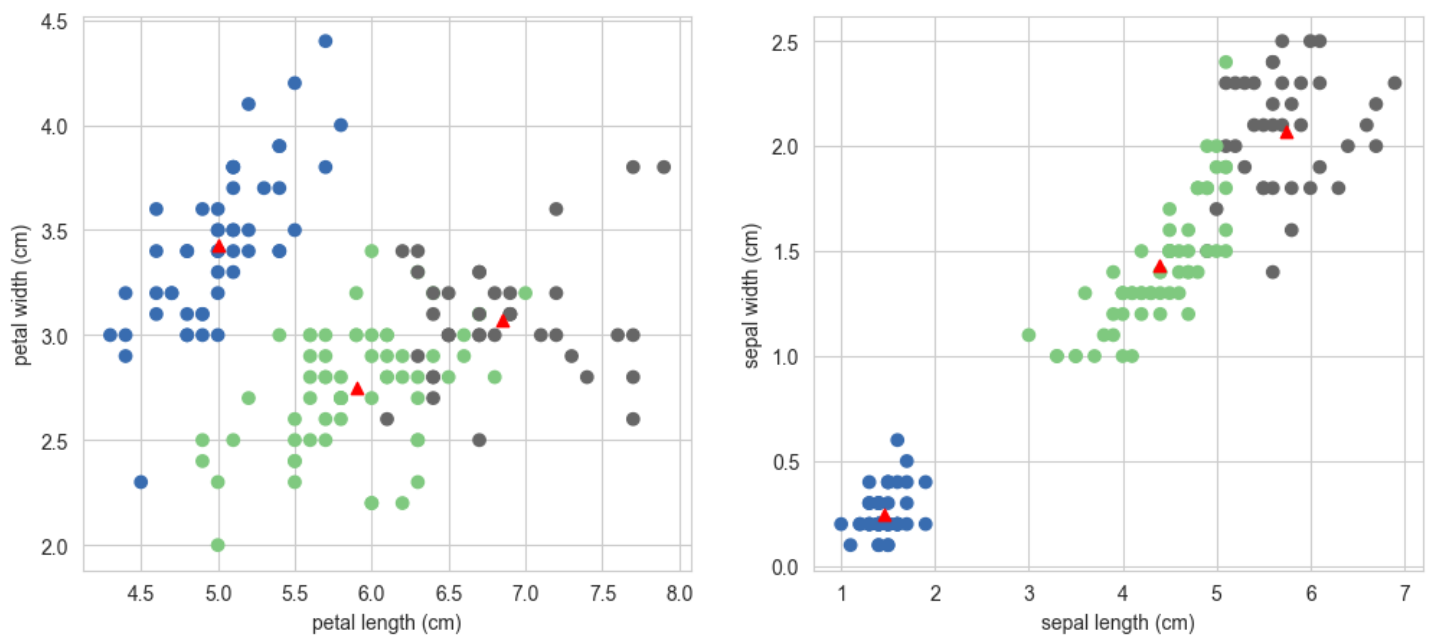
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
# 创建一个图形，设定其大小为宽 12 高 5
plt.figure(figsize=(12,5))

# 设置一行两列子图中的第一个子图。
plt.subplot(1, 2, 1)

# 根据数据 X 的第一列和第二列绘制散点图，用 pred 进行颜色映射，使用 cm.Accent 颜色映射表。
plt.scatter(X[:,0], X[:,1],c=pred, cmap=cm.Accent)

# 显示网格
plt.grid(True)

# 遍历 kmeans.cluster_centers_ 中的每个簇中心
for center in kmeans.cluster_centers_:
    # 取其前两维数据
	center = center[:2]

    # 用红色三角标记绘制这些簇中心
	plt.scatter(center[0],center[1],marker = '^',c = 'red')

# 设置第一个子图的 x 轴标签为“花瓣长度（厘米）”，y 轴标签为“花瓣宽度（厘米）”。
plt.xlabel("petal length (cm)")
plt.ylabel("petal width (cm)")


# 设置一行两列子图中的第二个子图。
plt.subplot(1, 2, 2)

# 根据数据 X 的第三列和第四列绘制散点图，用 pred 进行颜色映射，使用 cm.Accent 颜色映射表。
plt.scatter(X[:,2], X[:,3], c=pred, cmap=cm.Accent)

# 显示网格
plt.grid(True)

# 遍历 kmeans.cluster_centers_ 中的每个簇中心
for center in kmeans.cluster_centers_:
    # 取其前两维数据
	center = center[2:4]

    # 用红色三角标记绘制这些簇中心
	plt.scatter(center[0],center[1],marker = '^',c = 'red')

# 花的最外一轮叶状构造称为花萼。
# 设置第二个子图的 x 轴标签为“花萼长度（厘米）”，y 轴标签为“花萼宽度（厘米）”。
plt.xlabel("sepal length (cm)")
plt.ylabel("sepal width (cm)")
plt.show()

1715798449807

上一页
2024-09-11 16:03:49 #人工智能 #机器学习 #无监督学习
下一页