自然语言处理-循环神经网络(RNN BRNN LSTM GRU)
第一章 循环神经网络(RNN)
循环神经网络(Recurrent Neural Networks, RNNs)是一类特殊的神经网络。与传统的前馈神经网络不同,RNNs 的每一步输出都可以作为下一步的输入。例如,在预测一个句子的下一个单词时,需要依赖前面的单词,这就需要记住前面的单词信息,因此引入了 RNN。
RNNs 通过隐藏层来处理序列信息,其最重要的特征是隐藏状态,这一状态可以记住关于序列的部分信息,因此也被称为内存状态。隐藏状态能够记住网络先前的输入,使得 RNNs 可以对序列中的上下文信息进行建模。此外,RNNs 对每个输入使用相同的参数,因为它们对所有输入或隐藏层执行相同的任务来生成输出,这在一定程度上降低了参数的复杂性,与其他神经网络相比更加高效。
循环神经网络有着广泛的应用,包括但不限于以下领域:
- 语言建模和文本生成:RNNs 可以通过学习语言的结构和模式来生成自然语言文本。
- 语音识别:在语音领域,RNNs 能够处理连续的音频信号,实现语音识别。
- 机器翻译:RNNs 在翻译领域中能够根据前面的词生成相应的翻译,从而实现高质量的机器翻译。
- 序列相关的图像任务:例如视频分析,RNNs 能够处理图像序列并从中提取有用的信息。
- 时间序列预测:RNNs 在预测时间序列数据方面具有显著优势,如股票价格预测和气象预测。
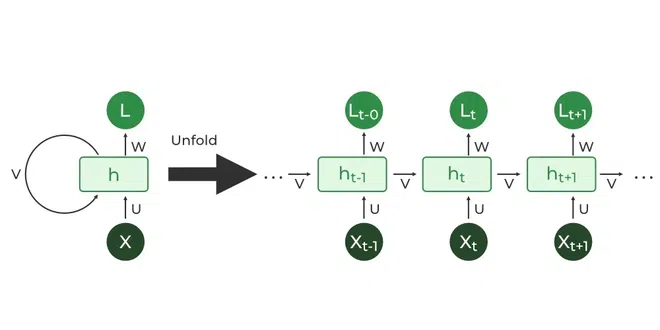
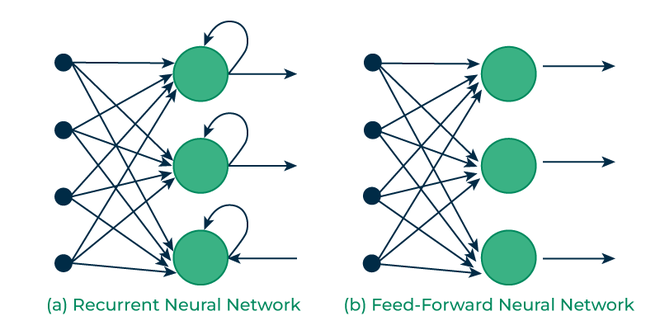
RNN 与前馈神经网络存在显著差异。所谓前馈神经网络,是指那种没有循环节点的人工神经网络,因其所有信息仅向前传递,故而也被称作多层神经网络。在前馈神经网络里,信息是从输入层单向地流向输出层(若存在隐藏层的话)。这类网络比较适合图像分类等任务,因为在这些情况下输入和输出是相互独立的。然而,它们无法对先前的输入进行保留,这就使得它们在进行顺序数据分析时作用较为有限。
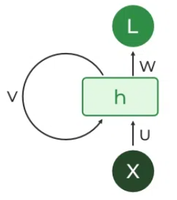
在循环神经网络(RNN)中,基本的处理单元并非明确被称作“循环神经元”,而是循环单元。此单元具备独特的保持隐藏状态的能力,能使网络在处理过程中通过记住先前输入来捕捉序列依赖关系。而长短期记忆(LSTM)和门控循环单元(GRU)等版本进一步提升了 RNN 处理长期依赖关系的能力。
第一节 循环神经网络的类型
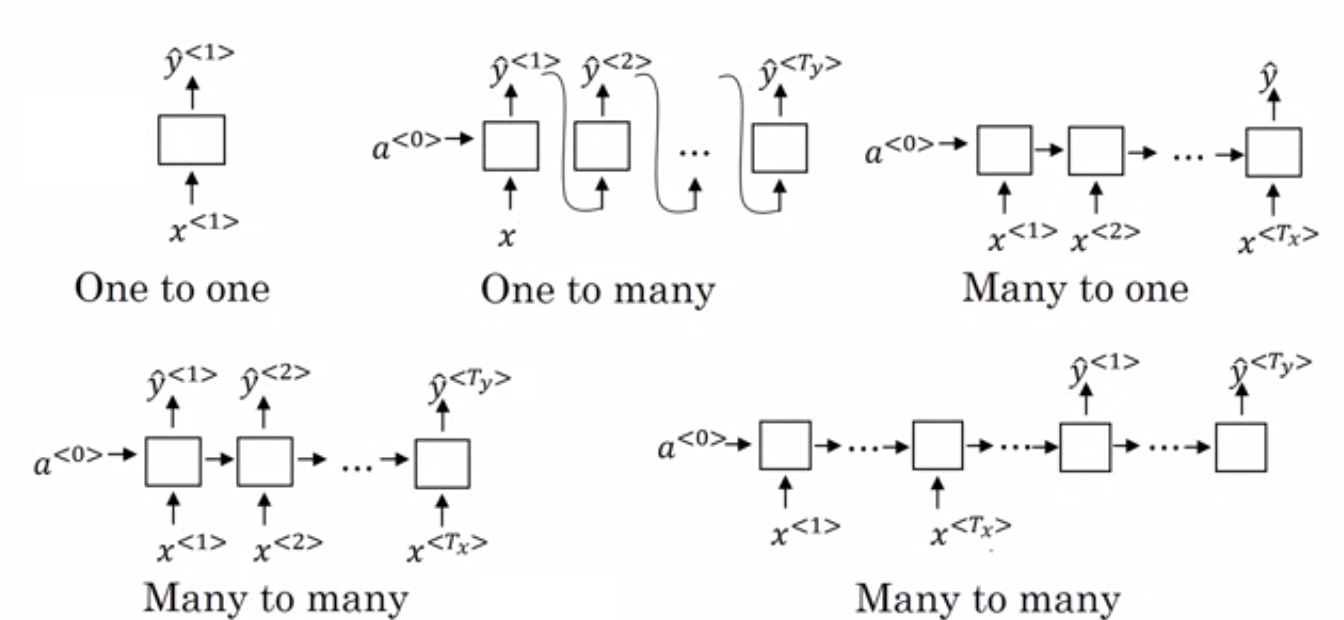
根据网络中输入和输出的数量,RNN 可以分为四种类型,每种类型适用于不同的应用场景:
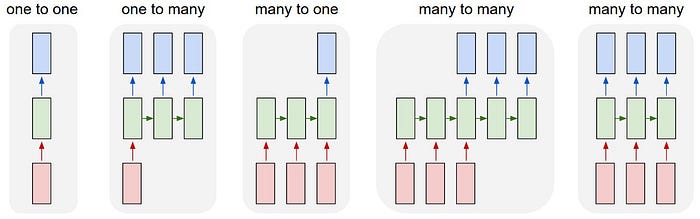
每个矩形代表向量,箭头代表函数。输入向量为红色,输出向量为蓝色,绿色保持 RNN 的状态。
| 类型 | 描述 | 应用场景 |
|---|---|---|
| 一对一 (One-to-One) | 一个输入对应一个输出 | 图像分类 |
| 一对多 (One-to-Many) | 一个输入生成一个序列输出 | 图像描述生成 |
| 多对一 (Many-to-One) | 输入一个序列生成一个输出 | 情感分析 |
| 多对多 (Many-to-Many) | 输入一个序列生成一个序列输出 | 机器翻译 |
1.1.1 循环神经网络的变体
| 类型 | 描述 | 应用示例 |
|---|---|---|
| 标准 RNN | 最基本的循环神经网络类型。每个时间步的输出依赖于前一个时间步的隐藏状态和当前输入。 | 简单序列预测 |
| 长短期记忆网络(LSTM) | 引入“遗忘门”、“输入门”和“输出门”来控制信息流动,解决长程依赖问题。 | 语言建模、文本生成 |
| 门控循环单元(GRU) | LSTM 的简化版本,只有两个门(更新门和重置门),结构更简单,计算效率更高。 | 机器翻译、语音识别 |
| 双向 RNN(Bi-directional RNN) | 包含两个独立的 RNN,一个从前向后处理序列,另一个从后向前处理序列。 | 语音识别、命名实体识别 |
| 深度 RNN(Deep RNN) | 将多个 RNN 层堆叠在一起形成更深的网络结构。 | 复杂序列建模 |
| 注意力机制和 Transformer | 基于注意力机制,不依赖循环结构,计算效率更高,适用于长序列。 | 机器翻译、文本摘要 |
| 回声状态网络(ESN) | 基于随机生成的隐藏层,并保持固定,通过调整输出层的权重进行训练。 | 动态系统建模 |
1.1.2 循环神经网络的优缺点
优点
- RNN能够记住所有时间点上的信息。这一特性使其在时间序列预测中非常有用,因为它能够记住先前的输入。这被称为长短期记忆(LSTM)。
- 循环神经网络甚至可以与卷积层结合,以扩展有效的像素邻域。
缺点
- 梯度消失和梯度爆炸问题。
- 训练RNN是一项非常困难的任务。
- 如果使用 $tanh$ 或 $relu$ 作为激活函数,它无法处理非常长的序列。
为了解决梯度消失和梯度爆炸问题,出现了几种新的高级RNN版本,包括:
- 双向神经网络(BiNN)
- 长短期记忆(LSTM)
第二节 循环神经网络架构
循环神经网络(RNN)与其他深度神经网络架构具有相同的输入和输出结构,但在信息从输入到输出的流动方式上存在差异。
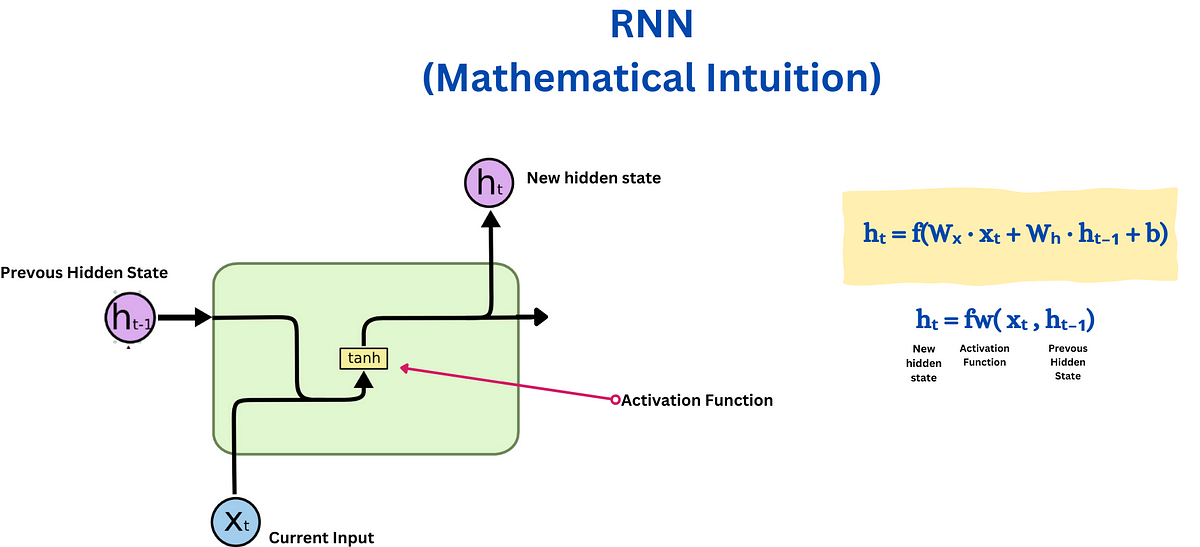
与传统深度神经网络不同,RNN 中的每个时间步使用相同的权重矩阵。也就是说,网络中的参数 $W, U, V, b, c$ 在所有时间步之间共享,而不是每层都有不同的权重矩阵。RNN 为每个输入 $X_i$ 计算隐藏状态 $H_i$。
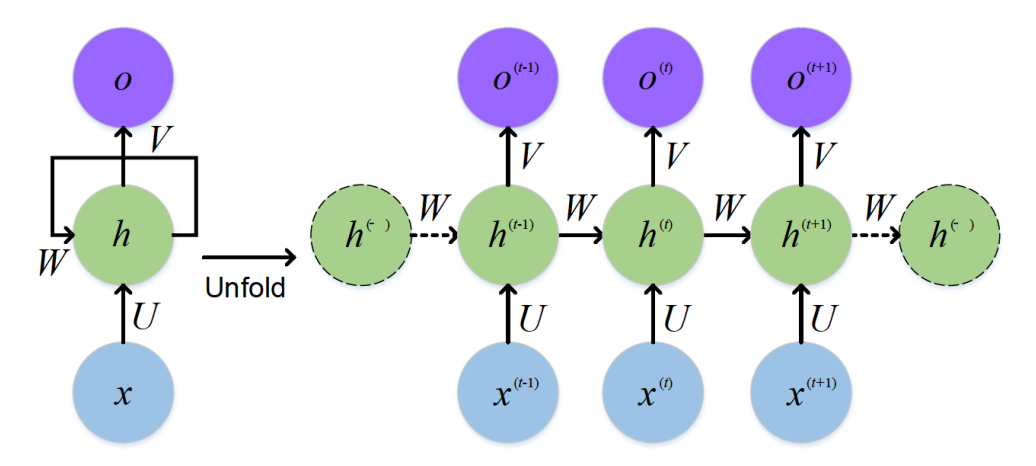
1.2.1 隐藏状态与输出的公式
隐藏状态计算:
$$ h_t = \sigma(U \cdot x_t + W \cdot h_{t-1} + b) $$其中:
- $h_t$ 是当前时间步 $t$ 的隐藏状态。
- $x_t$ 是当前时间步 $t$ 的输入。
- $h_{t-1}$ 是前一个时间步 $t-1$ 的隐藏状态。
- $U$ 是输入到隐藏状态的权重矩阵。
- $W$ 是隐藏状态到隐藏状态的权重矩阵。
- $b$ 是隐藏层的偏置向量。
- $\sigma$ 是激活函数(例如 sigmoid 函数)。
输出计算:
$$ O_t = Vh_t + c $$其中:
- $y_t$ 是当前时间步 $t$ 的输出。
- $V$ 是隐藏状态到输出的权重矩阵。
- $c$ 是输出层的偏置向量。
1.2.2 具体计算例子
假设有一个简单的RNN,输入序列 $\{x_1, x_2, x_3\}$,每个时间步的输入为一维向量。
RNN的参数如下:
- $U = 1.0$
- $W = 0.5$
- $b = 0.0$
- 激活函数为:$\tanh(x) = \frac{\sinh(x)}{\cosh(x)} = \frac{e^x - e^{-x}}{e^x + e^{-x}}$
初始隐藏状态 $h_0 = 0.0$。
输入序列: $\{1.0, 2.0, 3.0\}$
时间步1:
$$ x_1 = 1.0 $$ $$ \begin{aligned} h_1 &= \tanh(U \cdot x_1 + W \cdot h_0 + b) \\&= \tanh(1.0 \cdot 1.0 + 0.5 \cdot 0.0 + 0.0) \\&= \tanh(1.0) \\&= 0.7616 \end{aligned} $$时间步2:
$$ x_2 = 2.0 $$ $$ \begin{aligned} h_2 &= \tanh(U \cdot x_2 + W \cdot h_1 + b) \\&= \tanh(1.0 \cdot 2.0 + 0.5 \cdot 0.7616 + 0.0) \\&= \tanh(2.0 + 0.3808) \\&= \tanh(2.3808) \\&= 0.9825 \end{aligned} $$时间步3:
$$ x_3 = 3.0 $$ $$ \begin{aligned} h_3 &= \tanh(U \cdot x_3 + W \cdot h_2 + b) \\&= \tanh(1.0 \cdot 3.0 + 0.5 \cdot 0.9825 + 0.0) \\&= \tanh(3.0 + 0.49125) \\&= \tanh(3.49125) \\&= 0.9982 \end{aligned} $$最终隐藏状态:
$$ h_3 = 0.9982 $$通过这个例子,我们可以看到RNN如何逐步更新隐藏状态,并如何将序列数据的信息通过时间步传递。这个过程展示了RNN在处理序列数据时的优势,因为它能够记住之前时间步的信息并将其应用于当前时间步的计算中。
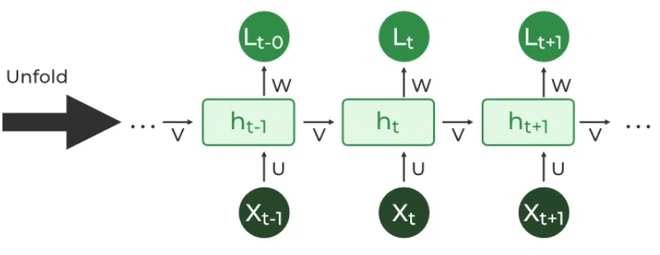
第三节 时间反向传播(BPTT)
时间反向传播(Backpropagation Through Time,BPTT)是一种用于训练循环神经网络(RNN)的算法。它是标准反向传播算法的一种变体,专门用于处理RNN中的时间特性。
在RNN中,每个时间步都有一个神经网络的副本,但是它们共享相同的权重。这意味着网络的输出取决于过去所有时间步的输入。BPTT通过展开RNN,将其看作是一个时间上的层叠网络,并在每个时间步应用标准的反向传播算法来计算梯度。
具体而言,BPTT通过将RNN展开到每个时间步,然后通过时间步骤依次向后传播误差来计算梯度。这意味着网络在每个时间步都会计算一个误差项,并将其传播回网络中,以更新权重。
BPTT的主要挑战之一是梯度消失或梯度爆炸问题,特别是当时间步骤很长时。这是因为误差在时间上会指数级地增长或衰减,从而使得更新的梯度变得不稳定。因此,在训练RNN时,通常需要采取一些技巧来解决这些问题,例如裁剪梯度或使用更复杂的循环单元结构,如长短期记忆(LSTM)或门控循环单元(GRU)。
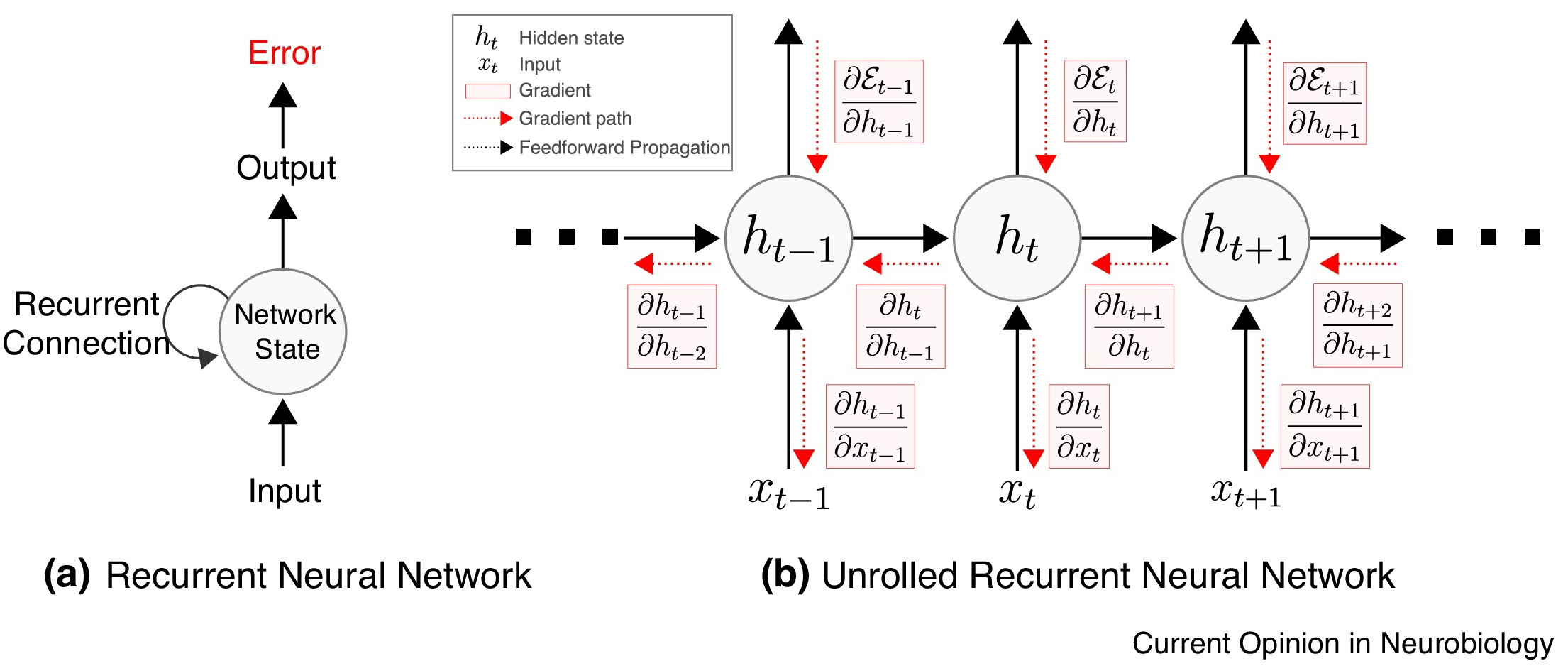
在循环神经网络中,神经网络是以一种有序的方式存在的,并且由于在有序网络中,每个变量是按照特定顺序依次计算的,比如先计算 h1,然后 h2,然后 h3 等等。因此,我们将在所有这些隐藏的时间状态中依次进行反向传播。
-1716533560100.webp)
损失函数 $L(\theta)$ 依赖于 $h_3$。
$h_3$ 依赖于 $h_2$ 和权重 $W$。 $h_2$ 依赖于 $h_1$ 和权重 $W$。 $h_1$ 依赖于 $h_0$ 和权重 $W$,其中 $h_0$ 是一个常数初始状态。 $$ \frac{\partial L(\theta)}{\partial W} = \sum_{t=1}^{T} \frac{\partial L(\theta)}{\partial W} $$为了简化这个方程,我们只对一行进行反向传播:
$$ \frac{\partial L(\theta)}{\partial W} = \frac{\partial L(\theta)}{\partial h_3} \cdot \frac{\partial h_3}{\partial W} $$如果我们知道如何计算这个,因为它与任何简单深度神经网络的反向传播相同。
在这样一个有序网络中,我们无法通过简单地将 $h_3$ 视为常数来计算 $\frac{\partial h_3}{\partial W}$,因为它也依赖于 $W$。总导数 $\frac{\partial h_3}{\partial W}$ 包含两个部分:
- 显式部分:将所有其他输入视为常数来计算 $\frac{\partial h_3^+}{\partial W}$
- 隐式部分:对 $h_3$ 到 $W$ 之间的所有间接路径求和。
1.3.1 计算过程
$$ \begin{aligned} \frac{\partial h_{3}}{\partial W} &= \frac{\partial h_{3}^+}{\partial W} + \frac{\partial h_{3}}{\partial h_{2}}\frac{\partial h_{2}}{\partial W} \\ &= \frac{\partial h_{3}^+}{\partial W} + \frac{\partial h_{3}}{\partial h_{2}} \left[\frac{\partial h_{2}^+}{\partial W} + \frac{\partial h_{2}}{\partial h_{1}}\frac{\partial h_{1}}{\partial W} \right] \\ &= \frac{\partial h_{3}^+}{\partial W} + \frac{\partial h_{3}}{\partial h_{2}}\frac{\partial h_{2}^+}{\partial W} + \frac{\partial h_{3}}{\partial h_{2}}\frac{\partial h_{2}}{\partial h_{1}} \left[\frac{\partial h_{1}^+}{\partial W} \right] \end{aligned} $$为了简化,我们将一些路径进行短路处理:
$$ \frac{\partial h_{3}}{\partial W} = \frac{\partial h_{3}^+}{\partial W} + \frac{\partial h_{3}}{\partial h_{2}}\frac{\partial h_{2}^+}{\partial W} + \frac{\partial h_{3}}{\partial h_{1}}\frac{\partial h_{1}^+}{\partial W} $$最终我们得到:
$$ \frac{\partial L(\theta)}{\partial W} = \frac{\partial L(\theta)}{\partial h_{3}} \cdot \frac{\partial h_{3}}{\partial W} $$其中:
$$ \frac{\partial h_{3}}{\partial W} = \sum_{k=1}^{3} \frac{\partial h_{3}}{\partial h_k} \cdot \frac{\partial h_k}{\partial W} $$因此,
$$ \frac{\partial L(\theta)}{\partial W} = \frac{\partial L(\theta)}{\partial h_{3}} \sum_{k=1}^{3} \frac{\partial h_{3}}{\partial h_k} \cdot \frac{\partial h_k}{\partial W} $$这种算法被称为时间上的反向传播(Backpropagation Through Time, BPTT),因为我们对所有之前的时间步进行反向传播。
1.3.2 标准RNN的问题
标准的循环神经网络(RNN)存在梯度消失和梯度爆炸问题的主要原因是长期依赖(Long-Term Dependencies)。
梯度消失(Gradient Vanishing):
- 在标准 RNN 中,梯度是通过时间步的连乘来传播的。如果在序列中存在长时间的依赖关系,即后续时间步的梯度会被连续相乘,如果这些值小于1,则梯度将会指数级地消失至接近于零,导致参数无法得到有效的更新。
- 这种情况通常出现在网络参数的权重矩阵 (W) 是小于1 的值(例如在使用 sigmoid 或 tanh 激活函数时)的情况下,尤其是在很多时间步后,这些值会趋近于零。
梯度爆炸(Gradient Exploding):
- 反之,如果权重矩阵 (W) 中的值大于1,则会导致梯度爆炸。在反向传播过程中,梯度会指数级地增加,导致梯度值变得非常大,这可能导致数值稳定性问题甚至网络参数溢出。
- 这种情况通常出现在网络参数的权重矩阵 (W) 是大于1 的值(例如在没有合适的梯度裁剪或正则化技术的情况下)的情况下,尤其是在存在很多时间步后。
用一个数学表达式来说明梯度消失和梯度爆炸的问题。
假设我们有一个简单的标准循环神经网络(RNN)模型,其隐藏状态的更新规则如下:
$$ H_t = \sigma(W_{hh} H_{t-1} + W_{xh} X_t + b_h) $$其中:
- $H_t$ 是时间步 $t$ 的隐藏状态。
- $W_{hh}$ 和 $W_{xh}$ 是隐藏状态和输入之间的权重矩阵。
- $b_h$ 是偏置项。
- $\sigma$ 是激活函数,例如 sigmoid 或 tanh。
假设我们使用均方误差(Mean Squared Error,MSE)作为损失函数:
$$ L = \frac{1}{2} \sum_{t=1}^T (Y_t - \hat{Y}_t)^2 $$其中:
- $Y_t$ 是模型在时间步 $t$ 的输出。
- $\hat{Y}_t$ 是时间步 $t$ 的目标输出。
我们来计算损失函数关于权重 $W_{hh}$ 的梯度:
$$ \frac{\partial L}{\partial W_{hh}} = \sum_{t=1}^T \frac{\partial L}{\partial H_t} \cdot \frac{\partial H_t}{\partial W_{hh}} $$ $$ \frac{\partial L}{\partial H_t} = (Y_t - \hat{Y}_t) $$ $$ \frac{\partial H_t}{\partial W_{hh}} = H_{t-1} \cdot \sigma'(W_{hh} H_{t-1} + W_{xh} X_t + b_h) $$其中 $\sigma'$ 是激活函数的导数。在这个例子中,我们使用的是 tanh 激活函数,其导数为 $\sigma'(x) = 1 - \sigma^2(x)$。
现在,我们假设 $W_{hh}$ 和 $W_{xh}$ 都是随机初始化的,且 $|W_{hh}| < 1$,表示 $W_{hh}$ 的绝对值小于1。在这种情况下,$\sigma'(W_{hh} H_{t-1} + W_{xh} X_t + b_h)$ 的值会在0到1之间。由于在反向传播过程中,梯度是通过时间步的连乘来传播的,如果梯度的值小于1,那么随着时间步的增加,梯度会指数级地减小,导致梯度消失问题。
随着指数的增大,$0.9$的幂次方会越来越接近 0,例如,$0.9^{10}\approx0.3487$,$0.9^{100}\approx0.00002656$,可以想象$0.9^{10000}$会是一个极小极小的值。
另一方面,如果 $|W_{hh}| > 1$,即 $W_{hh}$ 的绝对值大于1,那么 $\sigma'(W_{hh} H_{t-1} + W_{xh} X_t + b_h)$ 的值可能大于1。在反向传播过程中,梯度是通过时间步的连乘来传播的,如果梯度的值大于1,那么随着时间步的增加,梯度会指数级地增加,导致梯度爆炸问题。
随着指数的不断增大,$1.1$的幂次方会迅速增长。比如$1.1^{10}\approx2.5937$,$1.1^{100}\approx13780.6123$,可以想见$1.1^{10000}$会是一个极其巨大的数。
梯度消失和梯度爆炸问题限制了标准 RNN 在处理长序列和长期依赖关系时的性能。为了解决这些问题,出现了一些改进的 RNN 架构,如长短期记忆网络(LSTM)和门控循环单元(GRU)。这些架构通过引入门控机制来控制信息的流动,从而更有效地处理长期依赖关系,并且更稳定地训练。
1.3.3 梯度消失的例子
假设我们有一个非常简单的RNN,只有一个隐藏单元,激活函数是ReLU(虽然实际RNN通常使用tanh或sigmoid)。我们来看一个3步长的时间序列。
1.3.3.1 前向传播
- 隐藏状态更新公式:$h_t = \text{ReLU}(W_h h_{t-1} + W_x x_t)$
- 损失函数:$L = \sum_{t=1}^T L_t$
假设初始状态 $ h_0 = 0 $,权重 $ W_h = 0.5 $,输入 $ x_t = 1 $,时间步长 $ T = 3 $。
1.3.3.2 计算隐藏状态
- $ h_1 = \text{ReLU}(0.5 \cdot 0 + 1) = \text{ReLU}(1) = 1 $
- $ h_2 = \text{ReLU}(0.5 \cdot 1 + 1) = \text{ReLU}(1.5) = 1.5 $
- $ h_3 = \text{ReLU}(0.5 \cdot 1.5 + 1) = \text{ReLU}(1.75) = 1.75 $
1.3.3.3 反向传播
对于每一个时间步,我们需要计算梯度:
- $ \frac{\partial L}{\partial h_3} $
- $ \frac{\partial h_3}{\partial h_2} = \frac{\partial \text{ReLU}(0.5 \cdot h_2 + 1)}{\partial h_2} = 0.5 $
- $ \frac{\partial h_2}{\partial h_1} = 0.5 $
- $ \frac{\partial h_1}{\partial h_0} = 0.5 $
那么,梯度会是:
$$ \frac{\partial L}{\partial W_h} = \frac{\partial L}{\partial h_3} \cdot \frac{\partial h_3}{\partial h_2} \cdot \frac{\partial h_2}{\partial h_1} \cdot \frac{\partial h_1}{\partial h_0} = \frac{\partial L}{\partial h_3} \cdot (0.5)^3 $$当T很大时,比如 $ T = 10 $,我们得到:
$$ \frac{\partial L}{\partial W_h} = \frac{\partial L}{\partial h_{10}} \cdot (0.5)^{10} $$由于 $ (0.5)^{10} $ 是一个非常小的数(约为 0.000976),即使 $ \frac{\partial L}{\partial h_{10}} $ 是一个合理的数值,最终的梯度还是会非常小,这就是梯度消失的例子。
1.3.3.4 计算实例
同样的例子,但权重 $ W_h = 2 $,输入 $ x_t = 1 $,时间步长 $ T = 3 $。
计算隐藏状态:
- $ h_1 = \text{ReLU}(2 \cdot 0 + 1) = \text{ReLU}(1) = 1 $
- $ h_2 = \text{ReLU}(2 \cdot 1 + 1) = \text{ReLU}(3) = 3 $
- $ h_3 = \text{ReLU}(2 \cdot 3 + 1) = \text{ReLU}(7) = 7 $
反向传播:
同样的计算梯度:
- $ \frac{\partial L}{\partial h_3} $
- $ \frac{\partial h_3}{\partial h_2} = 2 $
- $ \frac{\partial h_2}{\partial h_1} = 2 $
- $ \frac{\partial h_1}{\partial h_0} = 2 $
那么,梯度会是:
$$ \frac{\partial L}{\partial W_h} = \frac{\partial L}{\partial h_3} \cdot 2^3 $$当 $T$ 很大时,比如 $ T = 10 $,我们得到:
$$ \frac{\partial L}{\partial W_h} = \frac{\partial L}{\partial h_{10}} \cdot 2^{10} $$由于 $ 2^{10} $ 是一个非常大的数(约为 1024),即使 $ \frac{\partial L}{\partial h_{10}} $ 是一个合理的数值,最终的梯度还是会非常大,这就是梯度爆炸的例子。
解决方法:
如前所述,为了解决这些问题,可以使用以下方法:
- 梯度裁剪:将梯度的值限制在一个合理范围内,以防止梯度爆炸。
- 权重初始化:采用适当的权重初始化方法,防止初始权重过大或过小。
- 高级RNN架构:使用LSTM或GRU,这些架构通过门控机制有效地控制信息流动,缓解梯度消失和爆炸问题。
第二章 双向循环神经网络(BRNN)
双向循环神经网络(Bidirectional Recurrent Neural Network,BRNN)是一种能够同时正向和反向处理输入数据的循环神经网络(RNN)。这种网络结构能够捕获输入数据中的上下文依赖关系,因为它不仅考虑过去的信息,还能够利用未来的信息。BRNN 通常用于自然语言处理(NLP)任务,如语言翻译、文本分类和命名实体识别。
BRNN 和循环神经网络的主要区别在于处理输入序列的方式。BRNN 能够同时考虑正向和反向的时间信息,因此在某些任务中具有优势,例如自然语言处理和语音识别。相比之下,标准的循环神经网络只能考虑过去的时间信息。
| 特征 | BRNN | 循环神经网络 (RNN) |
|---|---|---|
| 定义 | 双向循环神经网络。 | 循环神经网络。 |
| 目的 | 以正向和反向处理输入序列。 | 以单一方向处理输入序列。 |
| 输出 | 每个时间步骤的输出取决于过去和未来的输入。 | 每个时间步骤的输出仅取决于过去的输入。 |
| 训练 | 对前向和后向序列进行训练。 | 在单个序列上进行训练。 |
| 例子 | 自然语言处理任务,语音识别。 | 时间序列预测、语言翻译。 |
| 优点 | 提高处理顺序数据任务的性能。 | - 计算复杂度增加。 |
| 能够捕捉数据中的长期依赖关系。 | - 需要做更多优化工作。 | |
| 更好地处理复杂的输入序列。 | - 需要更长的输入序列。 |
第一节 为什么需要双向RNN
单向循环神经网络(RNN)只以单一方向处理输入序列,从左到右或从右到左。这意味着在后续时间步骤进行预测时,网络只能使用早期时间步骤的信息。这种限制可能导致网络无法捕获与输出预测相关的重要上下文信息。
例如,在自然语言处理任务中,前面的单词可能为当前单词提供了重要的上下文。如果使用单向 RNN,模型可能无法准确预测句子中的下一个单词。考虑以下例子:
- 苹果是我最喜欢的____。
- 苹果是我最喜欢的____,而且我在那里工作。
- 苹果是我最喜欢的____,我打算买一个。
在第一句中,答案可能是“水果”、“公司”或“电话”。但在第二句和第三句中,答案显然不能是“水果”。
只能从左到右处理输入的循环神经网络可能无法准确预测上述句子的正确答案。为了在自然语言任务中表现良好,模型必须能够双向处理序列。双向 RNN 能够同时从前向和后向处理输入数据,捕获更多的上下文信息,从而在复杂的语言任务中表现更好。
第二节 双向RNN拓扑图
BRNN 由两个独立的 RNN 组成:一个以正向处理输入数据,另一个以反向处理输入数据。最终输出是这两个方向的 RNN 输出的组合。组合方法可以是连接、逐元素加法或乘法,具体选择取决于任务的需求和预期输出的特性。
通过这种双向处理,BRNN 能够更全面地理解输入数据的上下文,从而在各种 NLP 任务中表现出色。
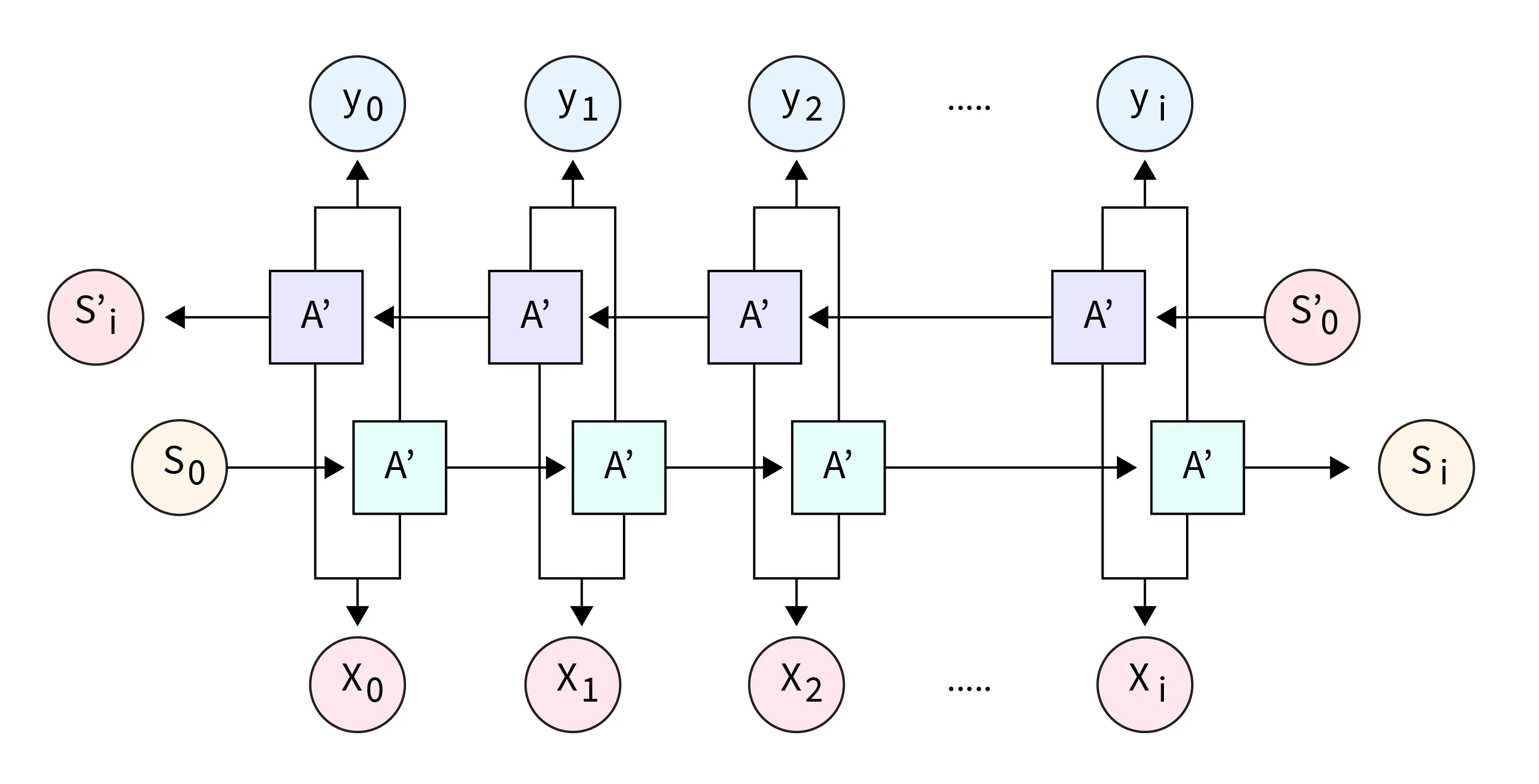
第三节 双向RNN中的合并模式
在双向循环神经网络(RNN)中,两个独立的 RNN 以相反的方向(前向和后向)处理输入数据。然后以某种方式将这两个 RNN 的输出组合或“合并”,以产生模型的最终输出。
有多种方法可以合并前向和后向 RNN 的输出,具体取决于模型的具体需求及其所要执行的任务。以下是一些常见的合并模式:
连接:在此模式下,前向和后向 RNN 的输出被连接在一起,从而产生一个长度为原始输入两倍的单个输出张量。
总计:在此模式下,前向和后向 RNN 的输出按元素相加,产生与原始输入具有相同形状的单个输出张量。
平均:在此模式下,前向和后向 RNN 的输出按元素进行平均,从而产生具有与原始输入相同形状的单个输出张量。
最大值:在此模式下,在每个时间步骤中取前向和后向输出的最大值,从而产生与原始输入具有相同形状的单个输出张量。
使用哪种合并模式取决于模型的具体需求和所要执行的任务。串联通常是一种很好的默认选择,在许多情况下效果很好,但其他合并模式可能更适合某些任务。
下图展示了一个沿着时间展开的双向循环神经网络。
每个时间步都重复利用六个独特的权重参数:
- 输入到向前和向后隐含层:$w1, w3 $
- 隐含层到自身:$w2, w5$
- 向前和向后隐含层到输出层:$w4, w6$
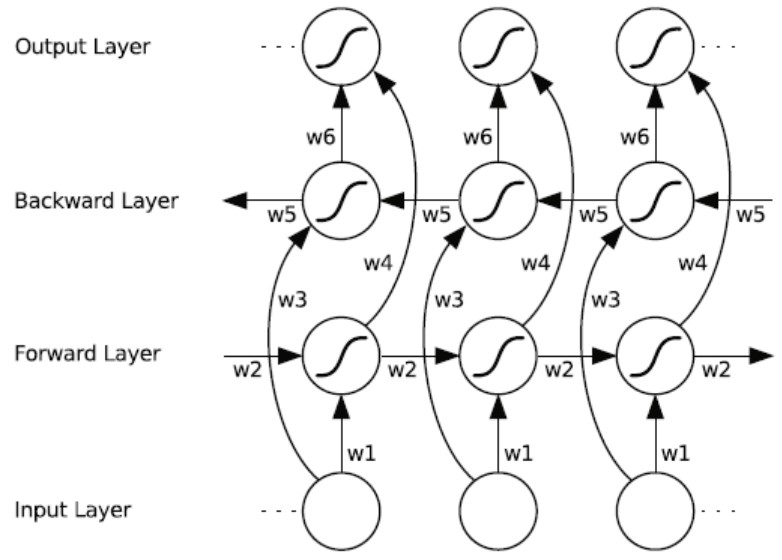
值得注意的是,向前和向后隐含层之间没有信息流动,这保证了展开的网络图是非循环的。每一个输出都是综合考虑两个方向的信息后得到的结果。
这个结构允许 BRNN 在每个时间步上都能利用整个输入序列的上下文信息,从而提高了模型的预测能力。
第四节 代码实例
2.4.1 TensorFlow版本
数据集说明:
IMDB 评论集是一个常用的自然语言处理数据集,由 IMDB(互联网电影数据库)收集和发布。该数据集包含了 IMDB 网站上用户对电影的评论,这些评论通常包含了用户对电影的观点、评价和评论。IMDB 评论集通常用于情感分析任务,即确定文本中的情感倾向,例如正面、负面或中性情感。
1 | import tensorflow as tf |
2.4.2 Pytorch版本
1 | import torch |
第三章 长短期记忆(LSTM)
从理论上讲,朴素连接的神经网络,即所谓的递归神经网络,可以工作。但在实践中,它存在两个问题:渐变消失和梯度爆炸,这使得它无法使用。
长短期记忆基于“读-写-忘”原则,网络根据输入信息读取和写入最有用的信息,并忘记对预测输出不重要的信息。为此,在RNN中引入了三个新的门控单元。通过这种方式,只有选择的信息会传递通过网络。
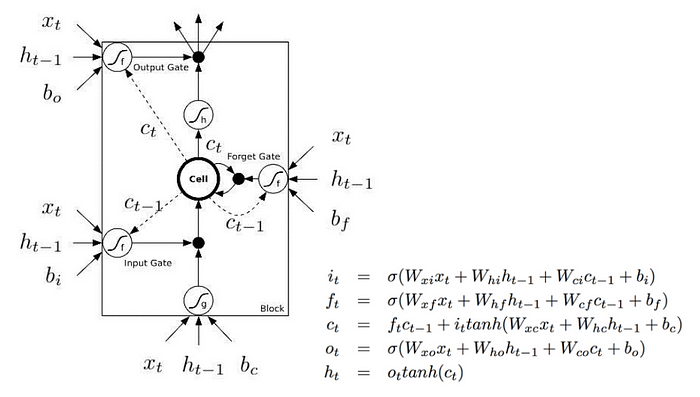
后来,LSTM(长短期记忆)被发明出来解决这个问题,通过在网络中明确引入一个称为单元的存储单元。这是 LSTM 构建基块的图示。
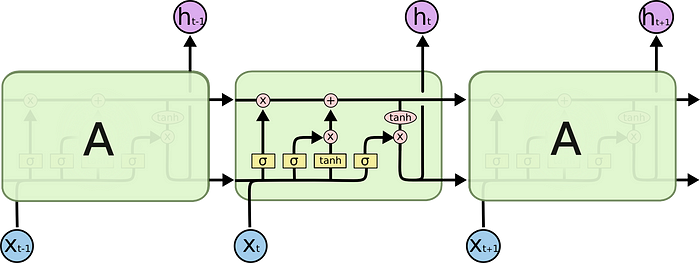
第一节 实现原理
如下图:乍一看,这看起来很吓人。让我们忽略内部结构,而只看设备的输入和输出。
该网络接受三个输入:
- $X_t$:是当前时间步长的输入
- $h_{t-1}$:是前一个 LSTM 单元的输出
- $C_{t-1}$:是前一个单元的“内存”,这被认为这是最重要的输入
至于输出:
- $h_t$:是当前网络的输出
- $C_t$: 是当前单元的内存
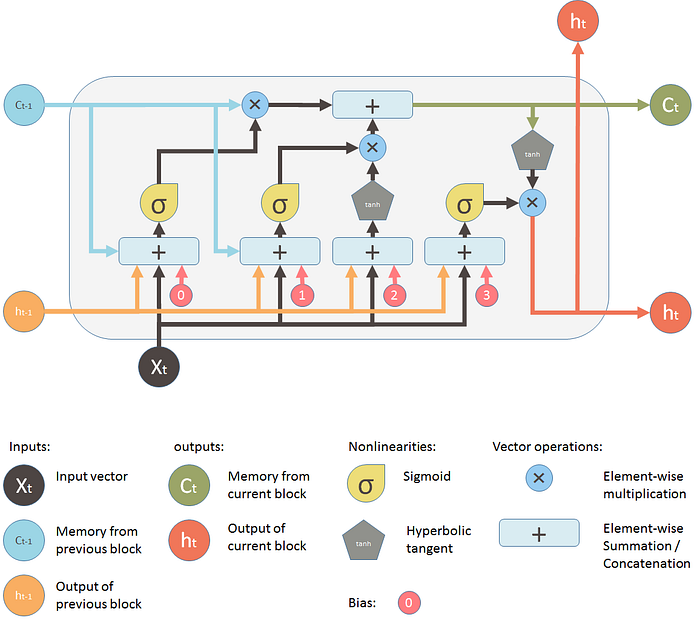
因此,这个单元通过考虑当前输入、先前的输出和先前的内存来做出决定。它会生成新的输出并更改其内存。
它的内部记忆 $C_t$ 变化的方式与通过管道输送水非常相似。假设内存是水,它会流入管道。您希望在此过程中更改此内存流,并且此更改由两个阀门控制。

3.1.1 遗忘门
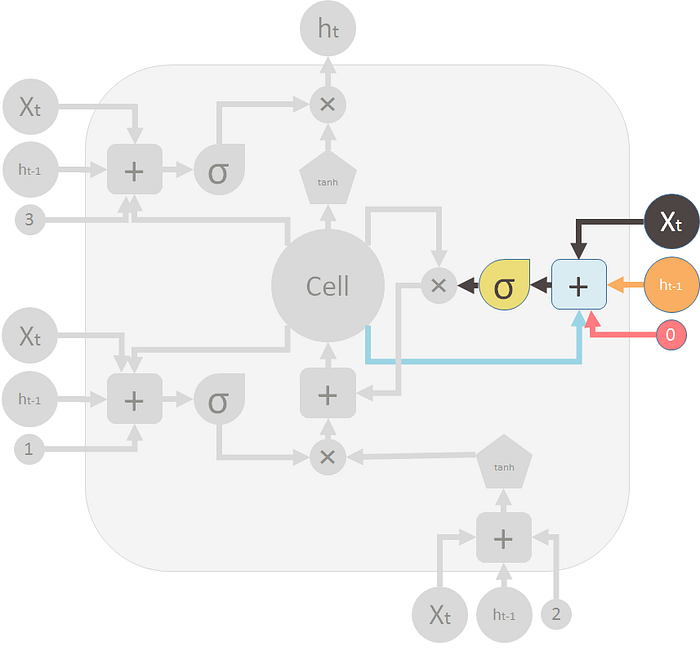
在 LSTM 图上,顶部的“管道”是记忆管道。输入是旧记忆(向量)。它通过的第一个 ✖️ 号是遗忘门。它实际上是一个元素相乘运算。
因此,如果将旧记忆 $C_{t-1}$ 乘以接近 $0$ 的向量,则意味着您要忘记大部分旧记忆。如果你的遗忘门等于 1,你就让旧的记忆通过。
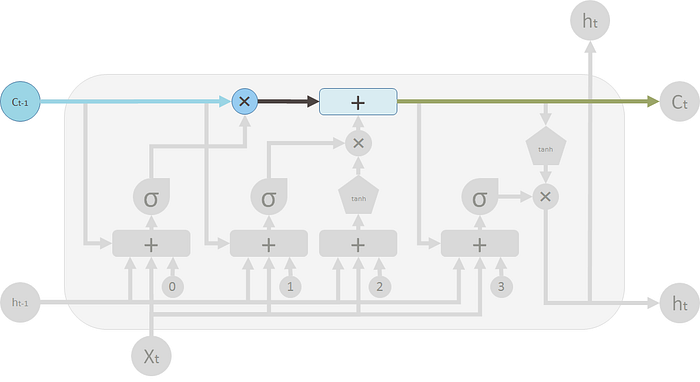
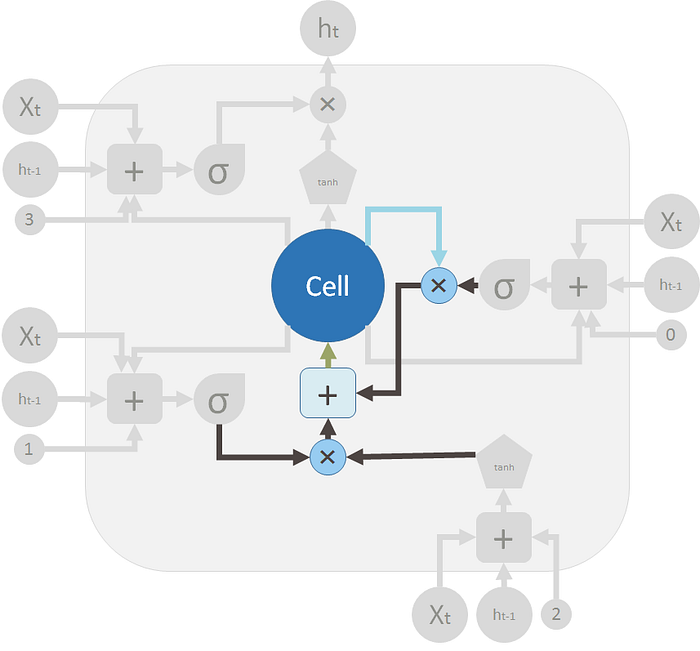
然后记忆流将经历的第二个操作是 $+$ 运算符。此运算符表示分段求和。它类似于 $T$ 形接头管。

新记忆和旧记忆将通过此操作合并。应向旧记忆添加多少新记忆由另一个阀门控制,即 $+$ 号下方的 ✖。执行这两个操作后,旧记忆 $C_{t-1}$ 将更改为新记忆$C_t$。
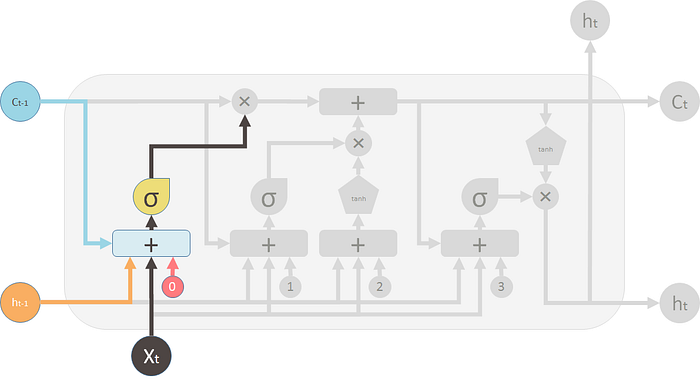
现在让我们看看阀门。第一个称为遗忘门。它由一个简单的单层神经网络控制。神经网络的输入是 $h_{t-1}$ 和 前一个 LSTM 模块的输出 $X_t$ 和 前一个模块的记忆 $C_{t-1}$ 以及 偏置向量 $b_0$ 。
该神经网络使用 sigmoid 作为激活函数,它的输出向量是遗忘门,通过逐元乘法应用于旧记忆 $C_{t-1}$。
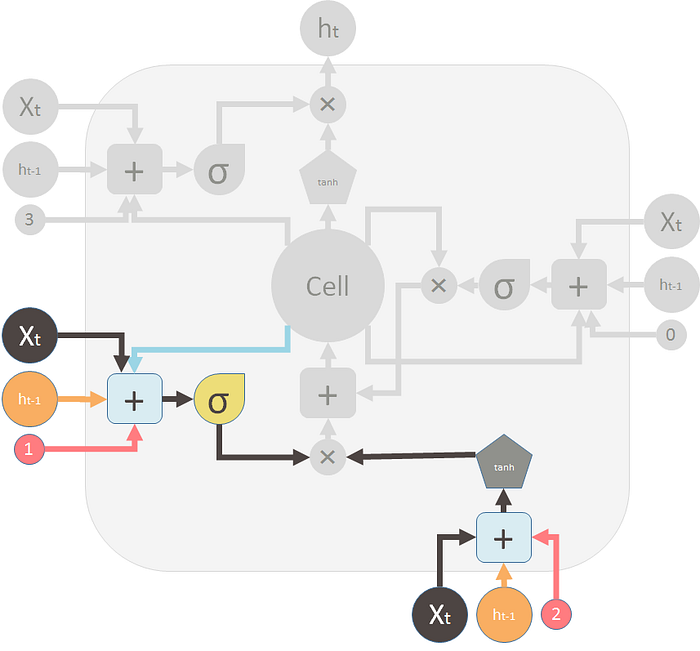
3.1.2 输入门
在 LSTM 中,第二个门被称为输入门(Input Gate)。它是一个单层简单的神经网络,接受与遗忘门相同的输入(前一时间步的隐藏状态和当前时间步的输入)。输入门控制新信息被添加到单元状态中的程度。
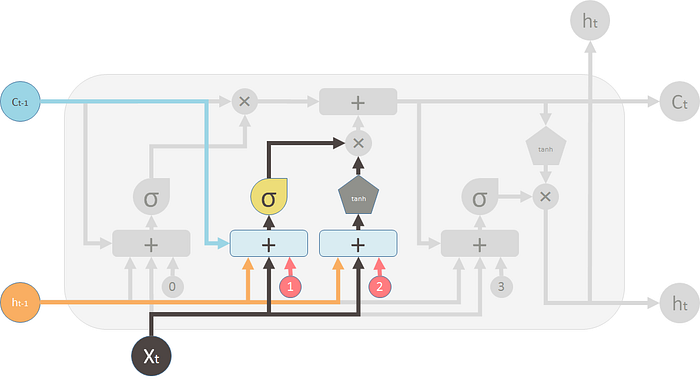
新的记忆内容本身是由另一个神经网络生成的,这个网络也是一个单层网络,但使用 tanh 作为激活函数。生成的新记忆内容会与输入门的输出逐元素相乘,然后与旧记忆结合,形成更新后的单元状态。
这两个✖标志分别是 遗忘门 和 输入门:
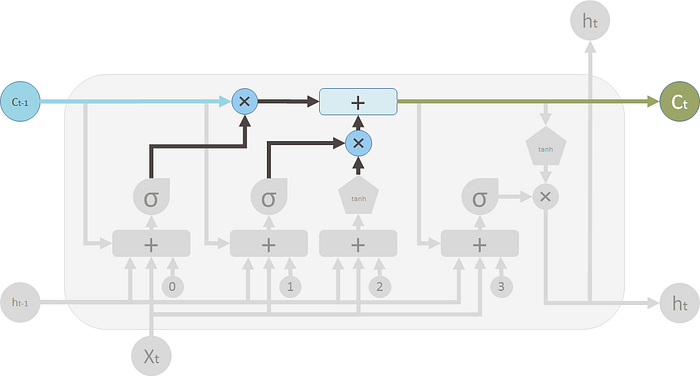
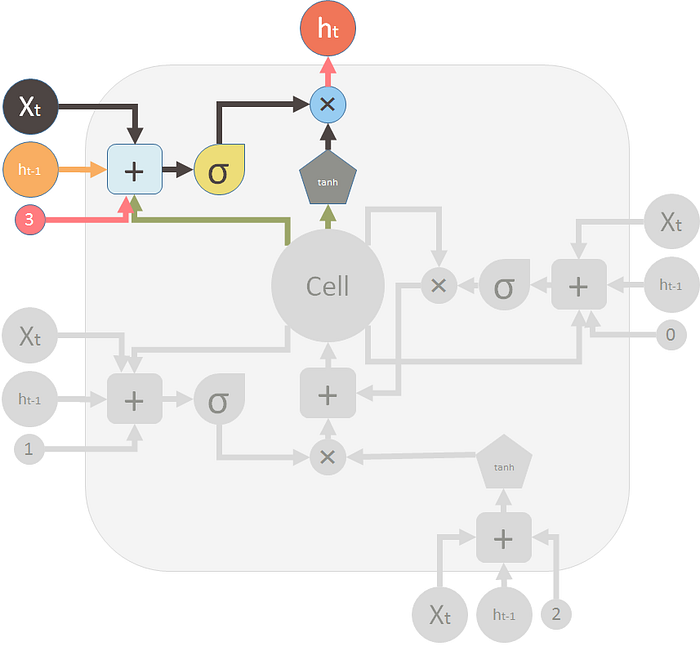
3.1.3 输出门
最后,我们需要为这个 LSTM 单元生成输出。这一步有一个输出门,该输出门是由新记忆 $C_t$ 、前一个时间步的输出 $h_{t-1}$、当前输入$X_t$ 和 偏置向量 $b_3$ 控制的输出门。这个输出门控制了新记忆应该输出多少信息到下一个 LSTM 单元。
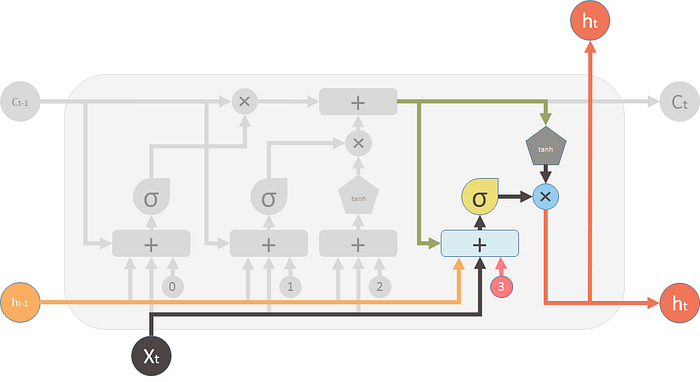
第二节 实现原理2
在这里,我想使用与第一张图相同的符号和颜色来重绘上图:
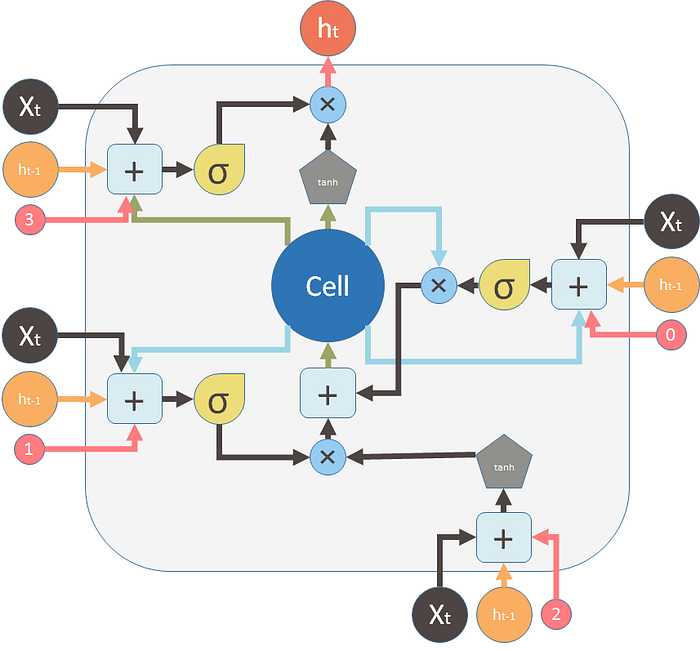
这是关闭旧记忆的遗忘门(阀门):
这是新的记忆门和新记忆:
这是两个阀门和元素求和,用于合并旧内存和新内存以形成$C_t$(绿色,流回大“单元”):
这是 LSTM 装置的输出阀和输出:
第三节 计算过程
LSTM 单元的核心组件包括遗忘门(Forget Gate)、输入门(Input Gate)、候选记忆状态(Candidate Memory Cell State)、输出门(Output Gate)和记忆单元状态(Cell State)。我们将通过具体的例子详细介绍每个步骤的数学计算过程。
假设我们有以下参数和输入:
- 输入向量 $x_t$ :[1.0, 0.5]
- 前一隐藏状态 $h_{t-1}$ :[0.0, 0.5]
- 前一记忆单元状态 $c_{t-1}$ :[0.1, 0.2]
- 权重矩阵和偏置项(这些是随意选择的以说明计算过程):
参数 值 注释 $W_f$ $\begin{bmatrix} 0.2 & 0.4 \\ 0.3 & 0.1 \end{bmatrix}$ 遗忘门的权重矩阵 $U_f$ $\begin{bmatrix}0.1 & 0.2 \\0.3 & 0.4\end{bmatrix}$ 遗忘门的偏置项 $b_f$ $[0.1, 0.1]$ 遗忘门的偏置项 $W_i$ $\begin{bmatrix}0.5 & 0.6 \\0.7 & 0.8\end{bmatrix}$ 输入门的权重矩阵 $U_i$ $\begin{bmatrix}0.3 & 0.4 \\0.5 & 0.6\end{bmatrix}$ 输入门的偏置项 $b_i$ $[0.2, 0.2]$ 输入门的偏置项 $W_c$ $\begin{bmatrix}0.6 & 0.5 \\0.4 & 0.3\end{bmatrix}$ 候选记忆状态的权重矩阵 $U_c$ $\begin{bmatrix}0.2 & 0.1 \\ 0.3 & 0.4\end{bmatrix}$ 候选记忆状态的偏置项 $b_c$ $[0.3, 0.3]$ 候选记忆状态的偏置项 $W_o$ $\begin{bmatrix}0.4 & 0.3 \\0.2 & 0.5\end{bmatrix}$ 输出门的权重矩阵 $U_o$ $\begin{bmatrix}0.1 & 0.2 \\0.3 & 0.4\end{bmatrix}$ 输出门的偏置项 $b_o$ $[0.1, 0.1]$ 输出门的偏置项
1. 遗忘门 (Forget Gate)
$$ f_t = \sigma(W_f x_t + U_f h_{t-1} + b_f) $$计算:
$$ W_f x_t = \begin{bmatrix} 0.2 & 0.4 \\ 0.3 & 0.1 \end{bmatrix} \begin{bmatrix} 1.0 \\ 0.5 \end{bmatrix} = \begin{bmatrix} 0.4 \\ 0.35 \end{bmatrix} $$ $$ U_f h_{t-1} = \begin{bmatrix} 0.1 & 0.2 \\ 0.3 & 0.4 \end{bmatrix} \begin{bmatrix} 0.0 \\ 0.5 \end{bmatrix} = \begin{bmatrix} 0.1 \\ 0.2 \end{bmatrix} $$ $$ W_f x_t + U_f h_{t-1} + b_f = \begin{bmatrix} 0.4 \\ 0.35 \end{bmatrix} + \begin{bmatrix} 0.1 \\ 0.2 \end{bmatrix} + \begin{bmatrix} 0.1 \\ 0.1 \end{bmatrix} = \begin{bmatrix} 0.6 \\ 0.65 \end{bmatrix} $$ $$ f_t = \sigma(\begin{bmatrix} 0.6 \\ 0.65 \end{bmatrix}) = \begin{bmatrix} \sigma(0.6) \\ \sigma(0.65) \end{bmatrix} = \begin{bmatrix} 0.6457 \\ 0.6570 \end{bmatrix} $$2. 输入门 (Input Gate)
$$ i_t = \sigma(W_i x_t + U_i h_{t-1} + b_i) $$计算:
$$ W_i x_t = \begin{bmatrix} 0.5 & 0.6 \\ 0.7 & 0.8 \end{bmatrix} \begin{bmatrix} 1.0 \\ 0.5 \end{bmatrix} = \begin{bmatrix} 0.8 \\ 1.1 \end{bmatrix} $$ $$ U_i h_{t-1} = \begin{bmatrix} 0.3 & 0.4 \\ 0.5 & 0.6 \end{bmatrix} \begin{bmatrix} 0.0 \\ 0.5 \end{bmatrix} = \begin{bmatrix} 0.2 \\ 0.3 \end{bmatrix} $$ $$ W_i x_t + U_i h_{t-1} + b_i = \begin{bmatrix} 0.8 \\ 1.1 \end{bmatrix} + \begin{bmatrix} 0.2 \\ 0.3 \end{bmatrix} + \begin{bmatrix} 0.2 \\ 0.2 \end{bmatrix} = \begin{bmatrix} 1.2 \\ 1.6 \end{bmatrix} $$ $$ i_t = \sigma(\begin{bmatrix} 1.2 \\ 1.6 \end{bmatrix}) = \begin{bmatrix} \sigma(1.2) \\ \sigma(1.6) \end{bmatrix} = \begin{bmatrix} 0.7685 \\ 0.8320 \end{bmatrix} $$3. 候选记忆状态 (Candidate Memory Cell State)
$$ \tilde{c}_t = \tanh(W_c x_t + U_c h_{t-1} + b_c) $$计算:
$$ W_c x_t = \begin{bmatrix} 0.6 & 0.5 \\ 0.4 & 0.3 \end{bmatrix} \begin{bmatrix} 1.0 \\ 0.5 \end{bmatrix} = \begin{bmatrix} 0.85 \\ 0.55 \end{bmatrix} $$ $$ U_c h_{t-1} = \begin{bmatrix} 0.2 & 0.1 \\ 0.3 & 0.4 \end{bmatrix} \begin{bmatrix} 0.0 \\ 0.5 \end{bmatrix} = \begin{bmatrix} 0.05 \\ 0.2 \end{bmatrix} $$ $$ W_c x_t + U_c h_{t-1} + b_c = \begin{bmatrix} 0.85 \\ 0.55 \end{bmatrix} + \begin{bmatrix} 0.05 \\ 0.2 \end{bmatrix} + \begin{bmatrix} 0.3 \\ 0.3 \end{bmatrix} = \begin{bmatrix} 1.2 \\ 1.05 \end{bmatrix} $$ $$ \tilde{c}_t = \tanh(\begin{bmatrix} 1.2 \\ 1.05 \end{bmatrix}) = \begin{bmatrix} \tanh(1.2) \\ \tanh(1.05) \end{bmatrix} = \begin{bmatrix} 0.8337 \\ 0.7807 \end{bmatrix} $$4. 更新记忆状态 (Memory Cell State)
$$ c_t = f_t \odot c_{t-1} + i_t \odot \tilde{c}_t $$计算:
$$ f_t \odot c_{t-1} = \begin{bmatrix} 0.6457 \\ 0.6570 \end{bmatrix} \odot \begin{bmatrix} 0.1 \\ 0.2 \end{bmatrix} = \begin{bmatrix} 0.06457 \\ 0.1314 \end{bmatrix} $$ $$ i_t \odot \tilde{c}_t = \begin{bmatrix} 0.7685 \\ 0.8320 \end{bmatrix} \odot \begin{bmatrix} 0.8337 \\ 0.7807 \end{bmatrix} = \begin{bmatrix} 0.6407 \\ 0.6495 \end{bmatrix} $$ $$ c_t = \begin{bmatrix} 0.06457 \\ 0.1314 \end{bmatrix} + \begin{bmatrix} 0.6407 \\ 0.6495 \end{bmatrix} = \begin{bmatrix} 0.7053 \\ 0.7809 \end{bmatrix} $$5. 输出门 (Output Gate)
$$ o_t = \sigma(W_o x_t + U_o h_{t-1} + b_o) $$计算:
$$ W_o x_t = \begin{bmatrix} 0.4 & 0.3 \\ 0.2 & 0.5 \end{bmatrix} \begin{bmatrix} 1.0 \\ 0.5 \end{bmatrix} = \begin{bmatrix} 0.55 \\ 0.45 \end{bmatrix} $$ $$ U_o h_{t-1} = \begin{bmatrix} 0.1 & 0.2 \\ 0.3 & 0.4 \end{bmatrix} \begin{bmatrix} 0.0 \\ 0.5 \end{bmatrix} = \begin{bmatrix} 0.1 \\ 0.2 \end{bmatrix} $$ $$ W_o x_t + U_o h_{t-1} + b_o = \begin{bmatrix} 0.55 \\ 0.45 \end{bmatrix} + \begin{bmatrix} 0.1 \\ 0.2 \end{bmatrix} + \begin{bmatrix} 0.1 \\ 0.1 \end{bmatrix} = \begin{bmatrix} 0.75 \\ 0.75 \end{bmatrix} $$ $$ o_t = \sigma(\begin{bmatrix} 0.75 \\ 0.75 \end{bmatrix}) = \begin{bmatrix} \sigma(0.75) \\ \sigma(0.75) \end{bmatrix} = \begin{bmatrix} 0.6792 \\ 0.6792 \end{bmatrix} $$6. 计算隐藏状态 (Hidden State)
$$ h_t = o_t \odot \tanh(c_t) $$计算:
$$ \begin{aligned} \tanh(c_t) &= \tanh(\begin{bmatrix} 0.7053 \\ 0.7809 \end{bmatrix}) \\&= \begin{bmatrix} \tanh(0.7053) \\ \tanh(0.7809) \end{bmatrix} \\&= \begin{bmatrix} 0.6071 \\ 0.6537 \end{bmatrix} \end{aligned} $$ $$ h_t = \begin{bmatrix} 0.6792 \\ 0.6792 \end{bmatrix} \odot \begin{bmatrix} 0.6071 \\ 0.6537 \end{bmatrix} = \begin{bmatrix} 0.4123 \\ 0.4441 \end{bmatrix} $$结果:
| 名称 | 值 |
|---|---|
| 输入 | [1.0, 0.5] |
| 前一隐藏状态 | [0.0, 0.5] |
| 前一记忆单元状态 | [0.1, 0.2] |
| 遗忘门输出 | [0.6457, 0.6570] |
| 输入门输出 | [0.7685, 0.8320] |
| 候选记忆状态 | [0.8337, 0.7807] |
| 当前记忆单元状态 | [0.7053, 0.7809] |
| 输出门输出 | [0.6792, 0.6792] |
| 当前隐藏状态 | [0.4123, 0.4441] |
第四节 代码实现
1 | import torch |
第四章 门控循环单元(GRU)
门控循环单元(GRU)是一种循环神经网络(RNN),于2014年由Cho等人提出,作为长短期记忆(LSTM)网络的更简单替代方案。与LSTM一样,GRU可用于处理文本、语音和时间序列等序列数据。
GRU的基本思想是使用门控机制在每个时间步骤选择性地更新网络的隐藏状态。门控机制用于控制信息进出网络的流动,包括重置门和更新门。

重置门决定了多少先前的隐藏状态应该被遗忘,更新门决定了多少新输入应该用来更新隐藏状态。
GRU的输出是根据更新后的隐藏状态计算出来的:
GRU的计算包括重置门 $r_t$、更新门 $z_t$ 和候选隐藏状态 $h_t'$ ,其方程式如下:
重置门:$r_t = \sigma(W_r \cdot [h_{t-1}, x_t])$
更新门:$z_t = \sigma(W_z \cdot [h_{t-1}, x_t])$
候选隐藏状态:$h_t' = \tanh(W_h \cdot [r_t \cdot h_{t-1}, x_t])$
隐藏状态:$h_t = (1 - z_t) \cdot h_{t-1} + z_t \cdot h_t'$
其中,$W_r$、$W_z$ 和 $W_h$ 是可学习的权重矩阵,$x_t$ 是时间步骤 $t$ 的输入,$h_{t-1}$ 是前一个隐藏状态,$h_t$ 是当前隐藏状态。
第一节 实现原理
4.1.1 更新门
我们首先使用以下公式计算 时间步长 $t$ 的更新门 $z_t$ :
$$ z_t = \sigma(W_{z}x_t+U_{z}h_{t-1}) $$当 $x_t$ 插入网络单元时,它会乘以自己的权重 $W_z$ 。$h_{t-1}$也是如此,它保存了前 $t-1$ 个单元的信息,并乘以自己的权重 $U_z$ 将两个结果相加,并应用 $ \sigma $ 激活函数将结果压缩到 $0$ 和 $1$ 之间。
按照上述模式,我们有:
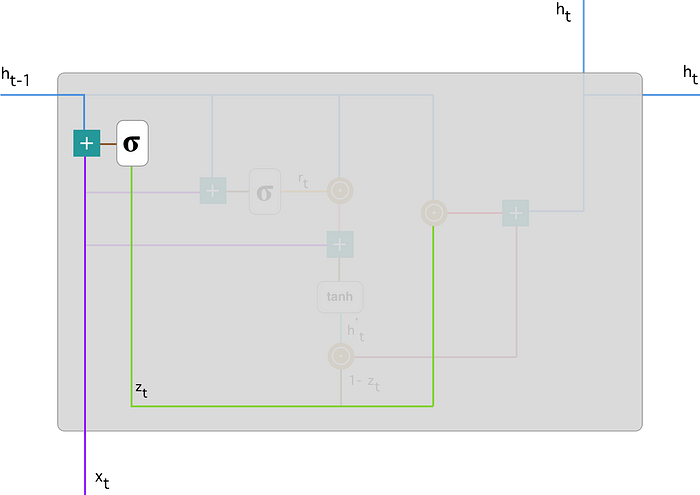
更新门帮助模型确定需要将多少过去的信息(来自先前的时间步骤)传递给未来。这非常强大,因为模型可以决定复制过去的所有信息并消除梯度消失问题的风险。稍后我们将看到更新门的用法。现在记住 $z_t$ 的公式。
4.1.2 重置门
本质上,这个重置门是用来决定要忘记多少过去的信息,为了计算它,我们使用:
$$ r_t=\sigma(W_{r}x_t + U_{r}h_{t-1}) $$此公式与更新门的公式相同。不同之处在于权重和门的用法,稍后会看到。下图显示了重置门的位置:
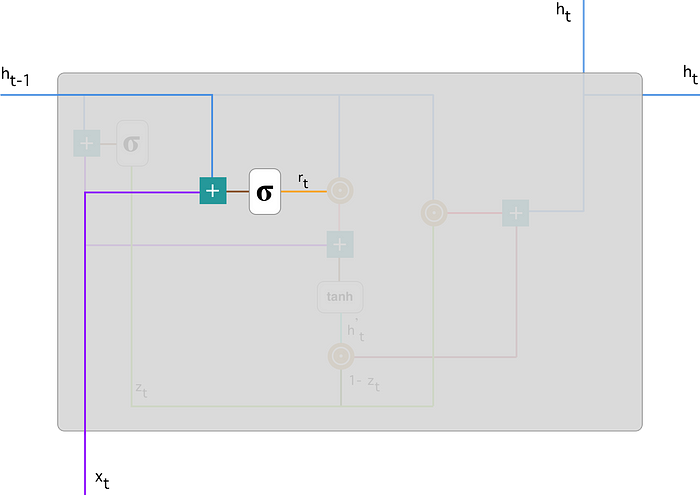
和以前一样,我们插入 蓝线:$h_{t-1}$ 和 紫线:$x_t$,将它们与相应的权重相乘,对结果求和并应用 $\sigma$ 激活函数。
4.1.3 当前记忆内容
让我们看看这些门究竟会如何影响最终的输出,首先,我们从重置门的使用开始。我们引入一个新的记忆内容,它将使用重置门来存储过去的相关信息。
它的计算方式如下:
$$ h_t^{'} = \tanh(Wx_t + r_t \odot U h_{t-1}) $$步骤:
- 将输入 $x_t$ 与权重 $W$ 相乘,将 $h_{t-1}$ 与权重 $U$ 相乘。
- 计算重置门 $r_t$ 和 $U h_{t-1}$ 之间的 Hadamard(逐元素)乘积。这将决定从前面的时间步骤中删除什么。
例如,在情感分析任务中,对于文本评论,我们可能只关心最后几句话的情感倾向,因此在网络接近文本末尾时,它将学会将重置门向量 $r_t$ 分配到接近 0 的位置,从而洗去过去的内容,只关注最后几句话。 - 将步骤 1 和 2 的结果相加。
- 应用非线性激活函数(如tanh)。
如图:我们对 蓝线:$h_{t-1}$和 橙线:$r_t$ 进行元素乘法,然后将结果 粉线 与输入 紫线:$x_t$ 相加。最后,使用 $tanh$ 生成 亮绿线:$h'_t$。
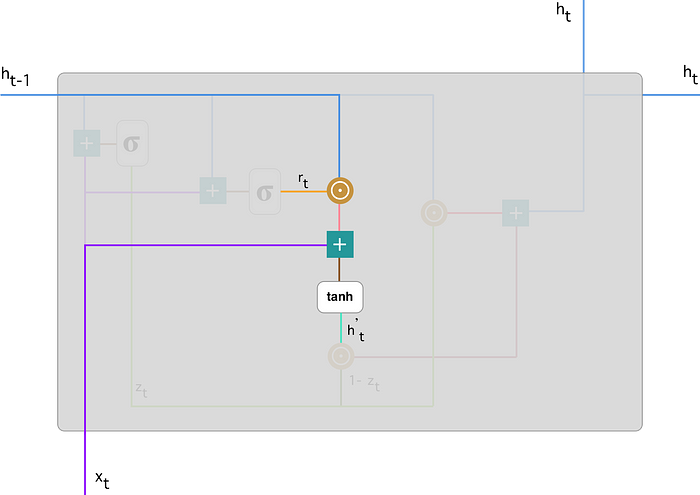
在数学中,符号 $\odot$ 通常表示两个数之间的哈达玛积(Hadamard product)或元素级乘法。哈达玛积是指对应位置上两个矩阵、向量或张量中的元素进行乘法操作,得到一个具有相同维度的新矩阵、向量或张量。
例如,如果有两个向量 $a = [a_1, a_2, a_3]$ 和 $b = [b_1, b_2, b_3]$,它们的哈达玛积 $a \odot b$ 将会得到一个新向量,其中每个元素都是对应位置上的两个向量元素的乘积,即:
$$ > a \odot b = [a_1 \cdot b_1, a_2 \cdot b_2, a_3 \cdot b_3] > $$哈达玛积在许多数学和工程应用中都是有用的,特别是在处理元素级别的操作时,如逐点函数应用和逐点加权。
4.1.4 当前时间步的最终记忆
作为最后一步,网络需要计算 $h_t$ — 保存当前单元信息的向量并将其传递给网络。
为此,需要更新门。它确定
- 从当前内存内容中收集什么 —— $h'_t$
- 从前面的步骤中收集什么 —— $h_{t-1}$。
具体操作如下:
$$ h_t = z_t \odot h_{t-1} + (1-z_t) \odot h'_t $$- 对更新门 $z_t$ 和 $h_{t-1}$ 应用元素乘法。
- 对$1-z_t$和 $h'_t$ 应用元素乘法。
- 将步骤 1 和 2 的结果相加。
让我们举一个关于书评的例子。这一次,最相关的信息位于文本的开头。模型可以学习将向量 $z_t$ 设置为接近 1,并保留大部分先前的信息。由于 $z_t$ 在此时间步骤中将接近 1,因此 $1-z_t$ 将接近 0,这将忽略当前内容的大部分(在本例中是评论的最后一部分,它解释了书的情节),这与我们的预测无关。
下面是强调上述等式的一个例子:
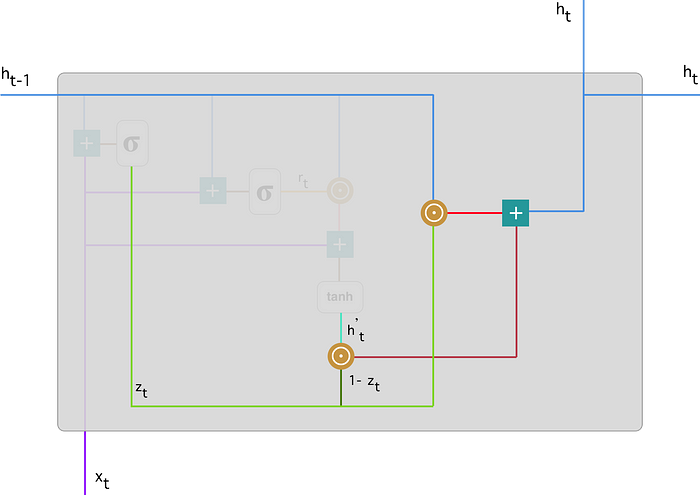
接下来,你会看到 绿线:$z_t$ 是如何计算 $1-z_t$ 的,它与 亮绿线:$h'_t$ 相结合,产生了 深红线 的结果。$z_t$ 还与 蓝线:$h_{t-1}$ 进行元素乘法。最后,蓝线:$h_t$ 是 亮红线 和 暗红线 对应输出相加的结果。
现在,您可以看到 GRU 如何使用其更新和重置门来存储和过滤信息。这消除了梯度消失问题,因为模型不会每次都清除新输入,而是保留相关信息并将其传递给网络的下一个时间步骤。如果经过精心训练,它们即使在复杂场景中也能表现得非常出色。
第二节 代码示例
1 | import numpy as np |
阅读扩展
第一节 RNN、DNN、CNN有什么不同?
RNN(循环神经网络)、DNN(深度神经网络)和CNN(卷积神经网络)是三种常见的神经网络结构,它们在网络结构、应用领域和处理方式上有所不同。
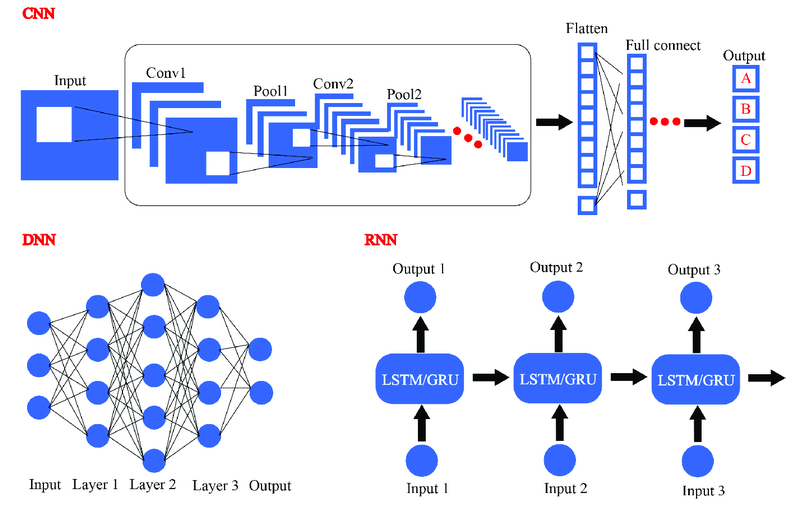
RNN(循环神经网络)
- 网络结构:RNN 主要用于处理序列数据,具有循环连接,可以在序列数据中捕捉时间上的依赖关系。在每个时间步,RNN 接收当前的输入和前一个时间步的隐藏状态,并生成新的隐藏状态和输出。
- 应用领域:适用于自然语言处理、语音识别、时间序列预测等需要处理序列数据的任务。
DNN(深度神经网络)
- 网络结构:DNN 是一种前馈神经网络,由多个全连接的隐藏层组成。每一层的神经元都与下一层的所有神经元相连,信息在网络中单向传递,没有循环连接。
- 应用领域:适用于图像分类、对象检测、语音识别等静态数据处理任务。
CNN(卷积神经网络)
- 网络结构:CNN 主要用于处理网格数据,如图像。它利用卷积层和池化层来提取特征,并通过全连接层进行分类或回归。
- 应用领域:适用于图像识别、目标检测、图像分割等与图像处理相关的任务。